题目内容
【题目】为了扶贫户学生好读书,读好书,某实验学校校友会在今年开学初,到新华书店采购文学名著和自然科学两类图书.经了解,购买30本文学名著和50本自然科学书共需2350元,20本文学名著比20本自然科学书贵500元.(注:所采购的文学名著价格都一样,所采购的自然科学书价格都一样)
(1)求每本文学名著和自然科学书的单价.
(2)若该校校友会要求购买自然科学书比文学名著多30本,自然科学书和文学名著的总数不低于80本,总费用不超过2400元,请求出所有符合条件的购书方案.
【答案】(1)每本文学名著45元,每本自然科学书20元;(2)方案一:文学名著25本,自然科学书55本;方案二:文学名著26本,自然科学书56本;方案三:文学名著27本,自然科学书57本.
【解析】
(1)设每本文学名著x元,每本自然科学书y元,根据题意列出方程组解答即可;
(2)根据学校要求购买自然科学书比文学名著多30本,自然科学书和文学名著的总数不低于80本,总费用不超过2400元,列出不等式组,解答即可.
解:(1)设每本文学名著x元,每本自然科学书y元,
可得:![]() ,
,
解得:![]() .
.
答:每本文学名著45元,每本自然科学书20元;
(2)设学校要求购买文学名著z本,自然科学书为(z+30)本,根据题意可得:
![]() ,
,
解得:![]() ,
,
因为x取整数,
所以x取25,26,27;
方案一:文学名著25本,自然科学书55本;
方案二:文学名著26本,自然科学书56本;
方案三:文学名著27本,自然科学书57本.

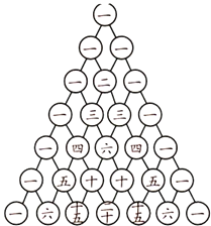
【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:
图① | 图② | 图③ | |
三个角上三个数的积 | 1×(﹣1)×2=﹣2 | (﹣3)×(﹣4)×(﹣5)=﹣60 |
|
三个角上三个数的和 | 1+(﹣1)+2=2 | (﹣3)+(﹣4)+(﹣5)=﹣12 |
|
积与和的商 | (﹣2)÷2=﹣1 |
|
|
(2)请用你发现的规律求出图④中的数x.