题目内容
运用所学的“幂的运算性质”am•an=am+n,am÷an=am-n,(am)n=amn,(ab)n=anbn.
(1)已知a=355,b=444,c=533,比较a、b、c的大小
(2)已知2a=3,2b=6,2c=12找出a、b、c之间的等量关系;
(3)试比较1714与3111的大小.
解:(1)∵a=355=(35)11=24311,b=444=(44)11=25611,c=533=(53)11=12511,
∴b>a>c;
(2)2的b次方=2的a次方×2=2的(a+1)次方,
即b=a+1,
2的c次方=2的a次方×4=2的(a+2)次方,
即c=a+2,
a+c=a+a+2=2a+2,
2b=2a+2=a+c
即a+c=2b,比较后,相等;
(3)∵1714>1614,
∴1714>256>255=3211,
∵3211>3111,
∴1714>3111.
分析:(1)从指数相同的幂,底数大的值大,很容易求得.
(2)从得数3,6,12中得到联系,2的b次方=2的a次方×2=2的(a+1)次方,即得.
(3)找到中间量,再找指数相同的幂,进行比较.
点评:本题考查了幂的乘方和积的乘方,(1)幂的指数相同,底数大小之间的比较;(2)在得数中得到联系,最终得到a,b,c之间的关系;(3)找到中间量,都同中间量进行比较.
∴b>a>c;
(2)2的b次方=2的a次方×2=2的(a+1)次方,
即b=a+1,
2的c次方=2的a次方×4=2的(a+2)次方,
即c=a+2,
a+c=a+a+2=2a+2,
2b=2a+2=a+c
即a+c=2b,比较后,相等;
(3)∵1714>1614,
∴1714>256>255=3211,
∵3211>3111,
∴1714>3111.
分析:(1)从指数相同的幂,底数大的值大,很容易求得.
(2)从得数3,6,12中得到联系,2的b次方=2的a次方×2=2的(a+1)次方,即得.
(3)找到中间量,再找指数相同的幂,进行比较.
点评:本题考查了幂的乘方和积的乘方,(1)幂的指数相同,底数大小之间的比较;(2)在得数中得到联系,最终得到a,b,c之间的关系;(3)找到中间量,都同中间量进行比较.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, 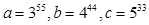 ,比较
,比较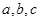 的大小
的大小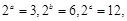 找出
找出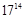 与
与 的大小.
的大小.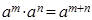 ,
,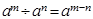 ,
, 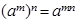 ,
,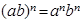 .
.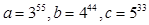 ,比较
,比较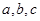 的大小
的大小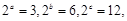 找出
找出 与
与 的大小.
的大小.