Question

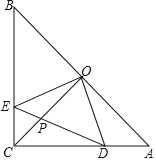
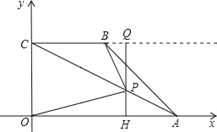
【题目】已知：直角梯形OABC中，CB∥OA，对角线OB和AC交于点D，OC=2，CB=2，OA=4，点P为对角线CA上的一点，过点P作QH⊥OA于H，交CB的延长线于点Q，连接BP，如果△BPQ和△PHA相似，则点P的坐标为______.

Answer 1

【答案】P()

【解析】

先根据点A、点C的坐标利用待定系数法求出直线AC的解析式，当△BQP∽△AHP时和△BQP∽△PHA时，利用相似三角形的性质就可以求出点P的坐标．

∵OC=2，OA=4，

∴C（0，2），A（4，0）．

设直线AC的解析式为y=kx+b，由题意，得，

解得，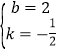

故直线AC的解析式为：y=﹣x+2．

∵QH⊥OA于H，交CB的延长线于点Q，

∴QH在点B的右侧，

如图：①当△BQP∽△AHP时，

则=，

∴BQPH=AHPQ．

∵点P在直线AC上，设点P的坐标为（x，﹣x+2）（0＜x＜4），

∴CQ=x，OH=x，PH=﹣x+2，

∵CB=2，OA=4，OH=2，

∴BQ=x﹣2，AH=4﹣x，PQ=x．

∴（x﹣2）（﹣x+2）=（4﹣x）（x），

解得x=4（舍去）．

②当△BQP∽△PHA时，

则，即BQAH=PHPQ，

（x﹣2）（4﹣x）=（﹣x+2）（x），

解得x1=，x2=4（舍去）

则y=，

则P（，）．

∴P（，）．

故答案为：P（，）．