题目内容
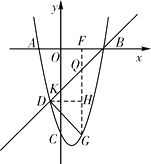
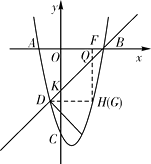
【题目】如图所示,已知抛物线经过点A(-2,0)、B(4,0)、C(0,-8),抛物线y=ax2+bx+c(a≠0)与直线y=x-4交于B , D两点.
(1)求抛物线的解析式并直接写出D点的坐标;
(2)点P为抛物线上的一个动点,且在直线BD下方,试求出△BDP面积的最大值及此时点P的坐标;
(3)点Q是线段BD上异于B、D的动点,过点Q作QF⊥x轴于点F , 交抛物线于点G . 当△QDG为直角三角形时,求点Q的坐标.
【答案】
(1)
设抛物线的解析式为y=ax2+bx+c
∵抛物线经过点A(-2,0)、B(4,0)、C(0,-8)
∴ 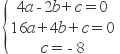 ,解得
,解得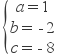 .
.
∴抛物线的解析式为y=x2-2x-8
点D的坐标为(-1,-5)
(2)
过P作PE∥y轴,交直线AB于点E
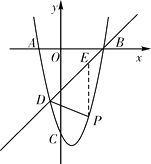
设P(x,x2-2x-8)则E(x,x-4)
∴PE=x-4-(x2-2x-8)=-x2+3x+4
∴S△BDP=S△DEP+S△BEP= ![]() PE·(xE-xD)+
PE·(xE-xD)+ ![]() PE·(xB-xE)
PE·(xB-xE)
= ![]() PE·(xB-xD)=
PE·(xB-xD)= ![]() PE=
PE= ![]() (-x2+3x+4)
(-x2+3x+4)
=- ![]() (x-
(x- ![]() )2+
)2+ ![]()
∴当x= ![]() 时,△BDP面积的最大值为
时,△BDP面积的最大值为 ![]()
此时点P的坐标为( ![]() ,-
,- ![]() )
)
(3)
设直线y=x-4与y轴相交于点K,则K(0,-4)
∵B(4,0),∴OB=OK=4,∴∠OKB=∠OBK=45°
∵QF⊥x轴,∴∠DQG=45°
若△QDG为直角三角形,则△QDG是等腰直角三角形
①∠QDG=90°,过D作DH⊥QG于H,∴QG=2DH,
∴-x2+3x+4=2(x+1),解得x 1=-1(舍去),
x 2=2,∴Q1(2,-2)
②∠DGQ=90°,则DH=QH,
∴-x2+3x+4=x+1,解得x 1=-1(舍去),x 2=3,∴P2(3,-1)
综上所述,当△QDG为直角三角形时,点Q的坐标为(2,-2)或(3,-1)
【解析】(1)设出一元二次函数,利用待定系数法求出a、b、c的值;
(2)设出PE两点的坐标,从图中可以看出SBDP=SEPB+SEPD.运用二次函数的性质求出SBDP的的最值及P点的坐标;
(3)一次函数为y=x-4,则意味着∠OKB=∠OBK=45°,则如果△QDG是直角三角形,必定是等腰直角三角形。但接下来要分两种情况去进行讨论:①∠QDG=90°;②∠DGQ=90°.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 名校课堂系列答案
名校课堂系列答案【题目】虽然近几年无锡市政府加大了太湖水治污力度,但由于大规模、高强度的经济活动和日益增加的污染负荷,使部分太湖水域水质恶化,富营养化不断加剧.为了保护水资源,我市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量(吨) | 单价(元/吨) |
不大于10吨部分 | 1.5 |
大于10吨不大于m吨部分(20≤m≤50) | 2 |
大于m吨部分 | 3 |
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
【题目】在一个不透明的盒子里装有40个黑、白两种颜色的球,这些球除颜色外完全相同.小丽做摸球实验,搅匀后她从盒子里摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,表是实验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
若从盒子里随机摸出一个球,则摸到白球的概率的估计值为 . (精确到0.1)