题目内容
【题目】如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2米高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13米的距离(点B,F,C在同一条直线上),则AE之间的长为_____米.(结果精确到lm,参考数据:sin22°≈0.375,cos22°≈0.9375,tan22°≈0.4)
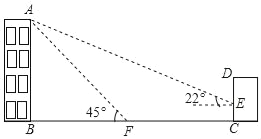
【答案】27
【解析】
首先构造直角三角形△AEM,利用tan22°=![]() ,即可求出教学楼AB的高度;再利用Rt△AME中,cos22°=
,即可求出教学楼AB的高度;再利用Rt△AME中,cos22°=![]() ,求出AE即可.
,求出AE即可.
过点E作EM⊥AB,垂足为M,如图所示:
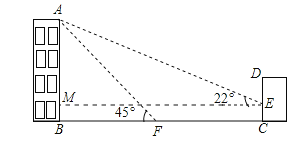 设AB为xm,
设AB为xm,
在Rt△ABF中,∠AFB=45°,
∴BF=AB=xm,
∴BC=BF+FC=(x+13)m,
在Rt△AEM中,AM=AB-BM=AB-CE=(x-2)m,
又tan∠AEM=![]() ,∠AEM=22°,
,∠AEM=22°,
∴![]() =0.4,
=0.4,
解得x≈12,
则ME=BC=BF+13≈12+13=25(m).
在Rt△AEM中,cos∠AEM=![]() ,
,
∴AE=![]() ,
,
故AE的长约为27m.
故答案是:27.

练习册系列答案
相关题目