题目内容
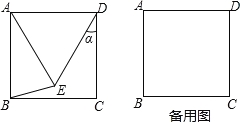
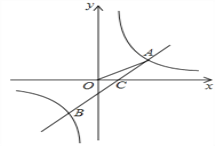
【题目】如图,反比例函数y=![]() 与反比例函数y=k2
与反比例函数y=k2![]() +b的图象的交点为A(m,1)、B(-2,n),OA与
+b的图象的交点为A(m,1)、B(-2,n),OA与![]() 轴正方向的夹角为α,且tanα=
轴正方向的夹角为α,且tanα=![]() 。
。
(1)求反比例函数及一次函数的表达式;
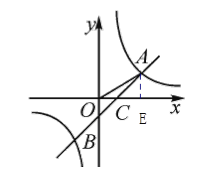
(2)设直线AB与x轴交于点C,且AC与x轴正方向的夹角为β,求tanβ的值。
【答案】(1)直线AB的解析式为y=![]() x-1;(2)
x-1;(2)![]() .
.
【解析】试题分析:(1)用待定系数法求函数表达式,需要知道图像上点的坐标,根据![]() ,构造直角三角形OAE,把三角函数值转化为边的比,可求出A点横坐标,把A坐标代入
,构造直角三角形OAE,把三角函数值转化为边的比,可求出A点横坐标,把A坐标代入![]() ,求得反比例函数解析式
,求得反比例函数解析式![]() ,把B坐标代入求出n=-2,把A、B坐标代入y=k2x+b即可求出一次函数解析式
,把B坐标代入求出n=-2,把A、B坐标代入y=k2x+b即可求出一次函数解析式![]() ;(2)易求C坐标(2,0),在Rt△ACE中,AE=1,CE=2,可求出tanβ的值.
;(2)易求C坐标(2,0),在Rt△ACE中,AE=1,CE=2,可求出tanβ的值.
试题解析:(1)过A作AE⊥x轴于E,∵tan∠AOE=tanα=![]() ,∴OE=4AE.又∵A(m,1),∴AE=1,AE=4,∴点A(4,1).∵A点在反比例函数
,∴OE=4AE.又∵A(m,1),∴AE=1,AE=4,∴点A(4,1).∵A点在反比例函数![]() 图像上,∴k1=4,∴反比例函数为
图像上,∴k1=4,∴反比例函数为![]() .∵B(-2,n)在反比例函数
.∵B(-2,n)在反比例函数![]() 图像上,∴n="-2." ∴B的坐标是(-2,-2), 将A,B两点的坐标代入直线y=k2x+b得:
图像上,∴n="-2." ∴B的坐标是(-2,-2), 将A,B两点的坐标代入直线y=k2x+b得: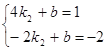 ,解得k2=
,解得k2=![]() ,b="-1," ∴直线AB的解析式为y=
,b="-1," ∴直线AB的解析式为y=![]() x-1;
x-1;
(2)∵直线AB的表达式为y=![]() x-1,令y=0,得x="2," ∴C(2,0), 又∵A(4,1),∴CE=2,AE=1.
x-1,令y=0,得x="2," ∴C(2,0), 又∵A(4,1),∴CE=2,AE=1.
∴tanβ=![]() =
=![]() .
.

练习册系列答案
相关题目