题目内容
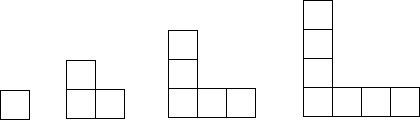
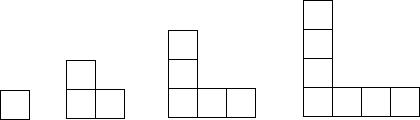
如图，搭第一个图形需要3根火柴棒．
（1）搭一搭，填一填：
（2）搭10个这样的三角形需要
（3）搭40个这样的三角形需要
（3）搭n个这样的三角形需要
（1）搭一搭，填一填：
| 三角形个数 | 1 | 2 | 3 | 4 | 5 | … |
| 火柴棒根数 | … |
21
21
根火柴棒．（3）搭40个这样的三角形需要
81
81
根火柴棒．（3）搭n个这样的三角形需要
2n+1
2n+1
根火柴棒．分析：观察不难发现，每增加一个三角形，需要增加2根火柴，然后写出前四个图形中的火柴的根数，再根据数据变化规律解答即可．
解答：解：第1个图形有3根火柴，
第2个图形有5根火柴，
第3个图形有7根火柴，
第4个图形有9根火柴，
…，
依此类推，第n个图形有2n+1根火柴；
（1）搭一搭，填一填：
（2）搭10个这样的三角形需要3+2×9=21根火柴棒．
（3）搭40个这样的三角形需要3+2×39=81根火柴棒．
（3）搭n个这样的三角形需要3+2（n-1）=2n+1根火柴棒．
故答案为：3，5，7，9，11；21；81；2n+1．
第2个图形有5根火柴，
第3个图形有7根火柴，
第4个图形有9根火柴，
…，
依此类推，第n个图形有2n+1根火柴；
（1）搭一搭，填一填：
| 三角形个数 | 1 | 2 | 3 | 4 | 5 | … |
| 火柴棒根数 | 3 | 5 | 7 | 9 | 11 | … |
（3）搭40个这样的三角形需要3+2×39=81根火柴棒．
（3）搭n个这样的三角形需要3+2（n-1）=2n+1根火柴棒．
故答案为：3，5，7，9，11；21；81；2n+1．
点评：本题是对图形变化规律的考查，比较简单，查出前几个图形中火柴的根数便不难得解．
练习册系列答案
相关题目
如图，搭第一个图形需要7根火柴棒．
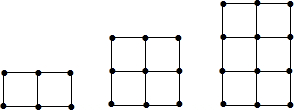
（1）搭一搭，填一填：
| 第几个图形 | 1 | 2 | 3 | 4 | 5 | … |
| 火柴棒根数 | … |
（3）搭30个图形需要______根火柴棒．
（3）搭n个图形需要______根火柴棒．
如图，搭第一个图形需要4根火柴棒，搭第二个图形需要10根火柴棒．
（1）搭一搭，填一填：
| 第几个图形 | 1 | 2 | 3 | 4 | … |
| 火柴棒根数 | … |
（3）搭30个图形需要______根火柴棒．
（4）搭n个图形需要______根火柴棒．
