题目内容
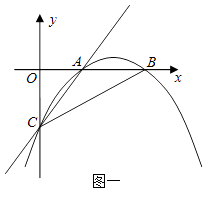
【题目】如图,抛物线y= ![]() x2+bx+c与x轴交于A、B两点,其中点B(2,0),交y轴于点C(0,﹣
x2+bx+c与x轴交于A、B两点,其中点B(2,0),交y轴于点C(0,﹣ ![]() ).直线y=mx+
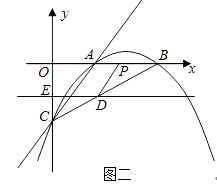
).直线y=mx+ ![]() 过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点(不与点B、D重合),过点P作y轴的平行线,交直线BD于点E,过点D作DM⊥y轴于点M.
过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点(不与点B、D重合),过点P作y轴的平行线,交直线BD于点E,过点D作DM⊥y轴于点M.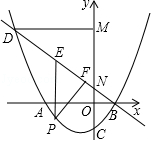
(1)求抛物线y= ![]() x2+bx+c的表达式及点D的坐标;
x2+bx+c的表达式及点D的坐标;
(2)若四边形PEMN是平行四边形?请求出点P的坐标;
(3)过点P作PF⊥BD于点F,设△PEF的周长为C,点P的横坐标为a,求C与a的函数关系式,并求出C的最大值.
【答案】
(1)
解:将B,C点坐标代入函数解析式,得 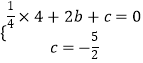 ,
,
解得 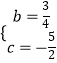 ,
,
抛物线的解析式为y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() .
.
∵直线y=mx+ ![]() 过点B(2,0),
过点B(2,0),
∴2m+ ![]() =0,
=0,
解得m=﹣ ![]() ,
,
直线的解析式为y=﹣ ![]() x+
x+ ![]() .
.
联立直线与抛物线,得 
∴ ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() =﹣
=﹣ ![]() x+
x+ ![]() ,
,
解得x1=﹣8,x2=2(舍),
∴D(﹣8,7 ![]() )
)
(2)
解:∵DM⊥y轴,
∴M(0,7 ![]() ),N(0,
),N(0, ![]() )
)
∴MN=7 ![]() ﹣
﹣ ![]() =6.
=6.
设P的坐标为(x, ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ),E的坐标则是(x,﹣
),E的坐标则是(x,﹣ ![]() x+
x+ ![]() )
)
PE=﹣ ![]() x+
x+ ![]() ﹣(
﹣( ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() )=﹣
)=﹣ ![]() x2﹣
x2﹣ ![]() x+4,
x+4,
∵PE∥y轴,要使四边形PEMN是平行四边形,必有PE=MN,
即﹣ ![]() x2﹣
x2﹣ ![]() x+4=6,解得x1=﹣2,x2=﹣4,
x+4=6,解得x1=﹣2,x2=﹣4,
当x=﹣2时,y=﹣3,即P(﹣2,﹣3),
当x=﹣4时,y=﹣ ![]() ,即P(﹣4,﹣
,即P(﹣4,﹣ ![]() ),
),
综上所述:点P的坐标是(﹣2,﹣3)和)(﹣4,﹣ ![]() )
)
(3)
解:在Rt△DMN中,DM=8,MN=6,
由勾股定理,得
DN= ![]() =10,
=10,
∴△DMN的周长是24.
∵PE∥y轴,
∴∠PEN=∠DNM,
又∵∠PFE=∠DMN=90°,
∴△PEF∽△DMN,
∴ ![]() =
= ![]() ,
,
由(2)知PE=﹣ ![]() a2﹣
a2﹣ ![]() a+4,
a+4,
∴ ![]() =
= ![]() ,
,
∴C=﹣ ![]() a2﹣
a2﹣ ![]() a+
a+ ![]() ,
,
C=﹣ ![]() (a+3)2+15,
(a+3)2+15,
C与a的函数关系式为C=﹣ ![]() a2﹣
a2﹣ ![]() a+
a+ ![]() ,
,
当x=﹣3时,C的最大值是15
【解析】(1)根据待定系数法,可得抛物线的解析式,直线的解析式,根据解方程组,可得D点坐标;(2)根据y轴上两点间的距离是较大的纵坐标减较小的纵坐标,可得MN,PE的长,根据平行四边形的判定,可得关于x的方程,根据解方程,可得P的横坐标,根据自变量与函数值的对应关系,可得答案;(3)根据勾股定理,可得DN的长,根据相似三角形的判定与性质,可得 ![]() =
= ![]() ,根据比例的基本性质,可得答案.
,根据比例的基本性质,可得答案.
【考点精析】掌握平行四边形的判定和相似三角形的判定与性质是解答本题的根本,需要知道两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案