题目内容
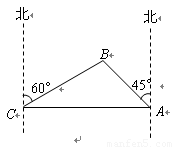
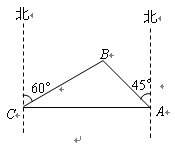
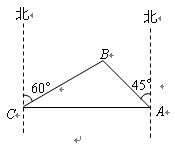
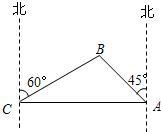 为打击索马里海盗,保护各国商船的顺利通行,我海军某部奉命前往该海域执行护航任务.某天我护航舰正在某小岛A北偏西45°并距该岛20海里的B处待命.位于该岛正西方向C处的某外国商船遭到海盗袭击,船长发现在其北偏东60°的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿BC航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置C处?(结果精确到个位.参考数据:
为打击索马里海盗,保护各国商船的顺利通行,我海军某部奉命前往该海域执行护航任务.某天我护航舰正在某小岛A北偏西45°并距该岛20海里的B处待命.位于该岛正西方向C处的某外国商船遭到海盗袭击,船长发现在其北偏东60°的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿BC航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置C处?(结果精确到个位.参考数据:| 2 |
| 3 |
分析:由条件可知△ABC为斜三角形,所以作AC上的高,转化为两个直角三角形求解.
解答:解:由图可知,∠ACB=30°,∠BAC=45°. (1分)
作BD⊥AC于D(如图).
在Rt△ADB中,AB=20,
∴BD=AB•sin45°=20×
=10
. (2分)
在Rt△BDC中,∠ACB=30°,
∴BC=2×10
=20
≈28. (3分)
∴
≈0.47. (4分)
∴0.47×60=28.2≈28(分钟). (5分)
答:我护航舰约需28分钟就可到达该商船所在的位置C.(6分)

作BD⊥AC于D(如图).
在Rt△ADB中,AB=20,
∴BD=AB•sin45°=20×
| ||
| 2 |
| 2 |
在Rt△BDC中,∠ACB=30°,
∴BC=2×10
| 2 |
| 2 |
∴
| 28 |
| 60 |
∴0.47×60=28.2≈28(分钟). (5分)
答:我护航舰约需28分钟就可到达该商船所在的位置C.(6分)
点评:化斜为直是解三角形的基本思路,因此需作垂线(高),原则上不破坏特殊角(30°、60°、45°).

练习册系列答案
相关题目
 北偏西
北偏西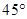 并距该岛
并距该岛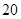 海里的
海里的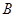 处待命.位于该岛正西方向
处待命.位于该岛正西方向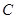 处的某外国商船遭到海盗袭击,船长发现在其北偏东
处的某外国商船遭到海盗袭击,船长发现在其北偏东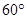 的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿
的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿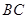 航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置
航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置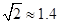 ,
,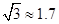 )
)
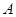 北偏西
北偏西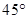 并距该岛
并距该岛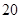 海里的
海里的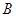 处待命.位于该岛正西方向
处待命.位于该岛正西方向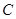 处的某外国商船遭到海盗袭击,船长发现在其北偏东
处的某外国商船遭到海盗袭击,船长发现在其北偏东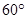 的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿
的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿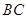 航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置
航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置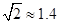 ,
, )
)
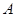 北偏西
北偏西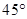 并距该岛
并距该岛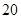 海里的
海里的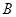 处待命.位于该岛正西方向
处待命.位于该岛正西方向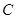 处的某外国商船遭到海盗袭击,船长发现在其北偏东
处的某外国商船遭到海盗袭击,船长发现在其北偏东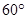 的方向有我军护航舰(如图9所示),便发出紧急求救信号.我护航舰接警后,立即沿
的方向有我军护航舰(如图9所示),便发出紧急求救信号.我护航舰接警后,立即沿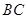 航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置
航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置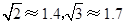 )
)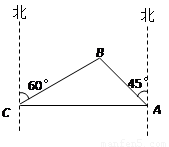
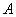 北偏西
北偏西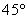 并距该岛
并距该岛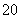 海里的
海里的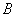 处待命.位于该岛正西方向
处待命.位于该岛正西方向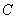 处的某外国商船遭到海盗袭击,船长发现在其北偏东
处的某外国商船遭到海盗袭击,船长发现在其北偏东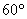 的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿
的方向有我军护航舰(如图所示),便发出紧急求救信号.我护航舰接警后,立即沿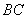 航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置
航线以每小时60海里的速度前去救援.问我护航舰需多少分钟可以到达该商船所在的位置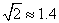 ,
,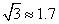 )
)