题目内容
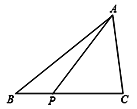
【题目】如图,P为△ABC边BC上的一点,且PC=2PB,已知∠ABC=45°,∠APC=60°,那么∠ACB的度数是 ( )
A. 45° B. 75° C. 90° D. 60°
【答案】B
【解析】试题解析:过C作AP的垂线CD,垂足为点D.连接BD;
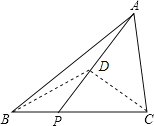
∵△PCD中,∠APC=60°,
∴∠DCP=30°,PC=2PD,
∵PC=2PB,
∴BP=PD,
∴△BPD是等腰三角形,∠BDP=∠DBP=30°,
∵∠ABP=45°,
∴∠ABD=15°,
∵∠BAP=∠APC-∠ABC=60°-45°=15°,
∴∠ABD=∠BAD=15°,
∴BD=AD,
∵∠DBP=45°-15°=30°,∠DCP=30°,
∴BD=DC,
∴△BDC是等腰三角形,
∵BD=AD,
∴AD=DC,
∵∠CDA=90°,
∴∠ACD=45°,
∴∠ACB=∠DCP+∠ACD=75°,
故选B.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目