题目内容
如图,矩形纸片ABCD中,BC=4,AB=3,点P是BC边上的动点(点P不与点B、C重合).现将△PCD沿PD翻折,得到△PC’D;作∠BPC’的角平分线,交AB 于点E.设BP= x ,BE= y,则下列图象中,能表示y与x的函数关系的图象大致是 ( )



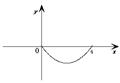

A B C D





A B C D
C
试题分析:根据题意,连接DE,因为△PCD沿PD翻折,得到△PC′D,故有DP平分∠CPC′;又PE为∠BPC′的角平分线,可推知∠EPD=90°,又因为BP=x,BE=y,BC=4,AB=3,分别用x和y表示出PD和EP和DE,在Rt△PED中利用勾股定理,即可得出一个关于x和y的关系式,化简即可.
:
 解:连接DE,
解:连接DE,△PCD沿PD翻折,得到△PC′D,故有DP平分∠CPC′;
又因为PE为∠BPC′的角平分线,
可推知∠EPD=90°,
已知BP=x,BE=y,BC=4,AB=3,
即在Rt△PCD中,PC=4-x,DC=3.即PD2=(4-x)2+9;
在Rt△EBP中,BP=x,BE=y,故PE2=x2+y2;
在Rt△ADE中,AE=3-y,AD=4,故DE2=(3-y)2+16
在Rt△PDE中,DE2=PD2+PE2
即x2+y2+(4-x)2+9=(3-y)2+16
化简得:
y=-(x2-4x);
结合题意,只有选项D符合题意.
故选C.
点评:本题主要考查了勾股定理的实际应用和对二次函数解析式的分析和读图能力,是一道不错的题目

练习册系列答案
相关题目
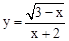 的自变量x的取值范围是 .
的自变量x的取值范围是 . 的图象与反比例函数
的图象与反比例函数 的图象交于
的图象交于 两点,与
两点,与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,已知
,已知 ,
, ,点
,点 的坐标为
的坐标为 .
.
 ,使得
,使得 与
与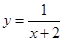 的自变量x的取值范围是 .
的自变量x的取值范围是 . )是函数图象上的最低点 请仔细观察甲、乙两图,解答下列问题
)是函数图象上的最低点 请仔细观察甲、乙两图,解答下列问题 
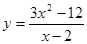 的值为零.
的值为零. 中,自变量x的取值范围是( )
中,自变量x的取值范围是( ) 中,自变量
中,自变量 的取值范围是( )
的取值范围是( )
 且
且 且
且