题目内容
如图，在直角坐标系中，已知点A（-3,4）、B(5,4），在x轴上找一点P，使PA+PB最小，则P点坐标为（ ）.
P（1,0）
解析试题分析：作A关于x轴的对称点A′，连接A′B与x轴相交于一点，根据轴对称-最短路线问题，交点即为所求的点P.可以求出直线A′B的解析式，令y=0可求出P点的横坐标，即可得解．如图，作A关于x轴的对称点A′（-3，-4），连接A′B与x轴相交于点P，则点P即为使PA+PB最短的点，设直线A′B的解析式为：y=kx+b把B(5,4）; A′（-3，-4）代入y=kx+b得：
，解得：
所以直线A′B的解析式为：y=x-1，令y=0得x=1.故点P的坐标为（1,0）.
考点：1、轴对称-最短路线问题.2、坐标与图形性质．
练习册系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
x的图象平行,则一次函数表达式为 。
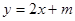不经过第二象限，那么实数
的取值范围是_________.
，则输出的函数值为 .