题目内容
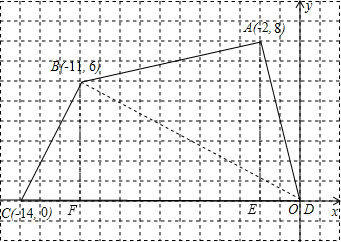
如图,四边形ABCD各个顶点的坐标分别为A(-2,8),B(-11,6),C(-14,0),D(0,0).
(1)求这个四边形ABCD的面积;
(2)如果把原来ABCD各个顶点纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?为什么?
(3)请你判断OB和BC是否垂直?请说明理由.

(1)求这个四边形ABCD的面积;
(2)如果把原来ABCD各个顶点纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?为什么?
(3)请你判断OB和BC是否垂直?请说明理由.

(1)过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,
则四边形ABCD的面积=
×(14-11)×6+
×(6+8)×(11-2)+
×2×8,
=9+63+8,
=80;
(2)所得的四边形面积不变.
因为原来四边形ABCD各个顶点纵坐标保持不变,横坐标增加2,就是把四边形ABCD向右平移2个单位,
所以,所得的四边形面积不变;
(3)根据勾股定理,BC2=(14-11)2+62=9+36=45,
OB2=112+62=121+36=157,
OC2=142=196,
∵45+157=202≠196,
∴BC2+OB2≠OC2,
∴OB和BC不垂直.
则四边形ABCD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=9+63+8,
=80;
(2)所得的四边形面积不变.
因为原来四边形ABCD各个顶点纵坐标保持不变,横坐标增加2,就是把四边形ABCD向右平移2个单位,
所以,所得的四边形面积不变;
(3)根据勾股定理,BC2=(14-11)2+62=9+36=45,
OB2=112+62=121+36=157,
OC2=142=196,
∵45+157=202≠196,
∴BC2+OB2≠OC2,
∴OB和BC不垂直.


练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目