题目内容
 如图,在一块边长为20米的正方形空地上种植草皮,草皮种植在大正方形的四个角上的相同的四个小正方形和中间与四个小正方形共顶点的一个小正方形上,当四个相同小正方形的边长为多少米时,草皮的面积为208平方米?
如图,在一块边长为20米的正方形空地上种植草皮,草皮种植在大正方形的四个角上的相同的四个小正方形和中间与四个小正方形共顶点的一个小正方形上,当四个相同小正方形的边长为多少米时,草皮的面积为208平方米?分析:首先假设小正方形边长,再根据已知表示出另一正方形边长,即可得出等式方程.
解答:解:设四个小正方形的边长为xm,根据题意得出:
4x 2+(20-2x) 2=208,
整理得:x 2-10x+24=0,
(x-4)(x-6)=0,
解得:x1=4 x2=6,
答:四个相同小正方形的边长为4米或6米时,草皮的面积为208平方米.
4x 2+(20-2x) 2=208,
整理得:x 2-10x+24=0,
(x-4)(x-6)=0,
解得:x1=4 x2=6,
答:四个相同小正方形的边长为4米或6米时,草皮的面积为208平方米.
点评:此题主要考查了一元二次方程的应用,根据已知得出中间正方形的边长是解题关键.

练习册系列答案
相关题目
 29、如图,在一块边长为acm的正方形纸板中,四个角分别剪去一个边长为bcm的小正方形,利用因式分解计算:当a=98cm,b=27cm时,剩余部分的面积是多少?
29、如图,在一块边长为acm的正方形纸板中,四个角分别剪去一个边长为bcm的小正方形,利用因式分解计算:当a=98cm,b=27cm时,剩余部分的面积是多少?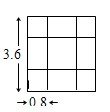 12、如图,在一块边长为3.6cm的正方形纸片的四角,各剪去一个边长为0.8cm的正方形,则剩余部分的面积是
12、如图,在一块边长为3.6cm的正方形纸片的四角,各剪去一个边长为0.8cm的正方形,则剩余部分的面积是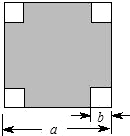 如图,在一块边长为acm的正方形纸板四角,各剪去一个边长为bcm(b<
如图,在一块边长为acm的正方形纸板四角,各剪去一个边长为bcm(b< 如图,在一块边长为a厘米的正方形纸板四角,各剪去一个边长为b(b<
如图,在一块边长为a厘米的正方形纸板四角,各剪去一个边长为b(b<