题目内容
操作示例
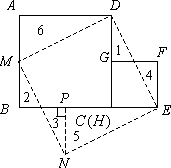
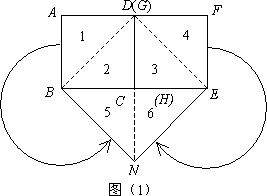
对于边长均为α的两个正方形ABCD和EFGH，按图(1)所示的方式摆放，再沿虚线BD，EG剪开后，可以按图中所示的移动方式拼接为图(1)中的四边形BNED．
从拼接的过程容易得到结论：
①四边形BNED是正方形；
②S正方形ABCD＋S正方形EFGH＋S正方形BMED．
实践与探究
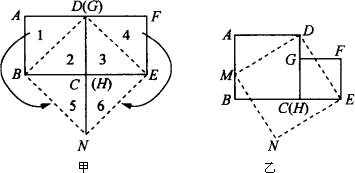
(1)对于边长分别为a，b(a＞b)的两个正方形ABCD和EFGH，按图(2)所示的方式摆放，连结DE，过点D作DM⊥DE，交AB于点M，过点M作MN⊥DM，过点E作EN⊥DE，MN与EN相交于点N．
①证明四边形MNED是正方形，并用含a，b的代数式表示正方形MNED的面积；
②在图(2)中，将正方形ABCD和正方形EFGH沿虚线剪开后，能够拼接为正方形MNED．请简略说明你的拼接方法(类比图(1)，用数字表示对应的图形)．
(2)对于n(n是大于2的自然数)个任意的正方形，能否通过若干次拼接，将其拼接为一个正方形？请简要说明你的理由．
答案：
解析：
解析：
|
(1)①证明：由作图的过程可知四边形 ②过点 可以证明图中6与5位置的两个直角三角形全等，4与3位置的两个直角三角形全等，2与1位置的两个直角三角形也全等．所以将6放到5的位置，4放到3的位置，2放到１的位置，恰好拼接为正方形
(2)答：能． 理由是：由上述的拼接过程可以看出：对于任意的两个正方形都可以拼接为一个正方形，而拼接出的这个正方形可以与第三个正方形再拼接为一个正方形， |
是矩形．在Ｒt△
与Ｒt△
中，
，
．
Rt△
Rt△
．
．
，
；
，
，如图．
依次类推．由此可知：对于
个任意的正方形，可以通过
次拼接，得到一个正方形．
练习册系列答案
相关题目
