题目内容
【题目】如图，已知∠AOB=60°，点P是OA边上，OP=8cm，点M、N在边OB上，PM=PN，若MN=2cm，则ON=cm．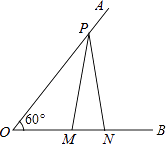 
【答案】5
【解析】解：过P作PD⊥OB于点D， 在Rt△OPD中，∵∠ODP=90°，∠POD=60°，
∴∠OPD=30°，
∴OD= 
OP= ×8=4cm，
∵PM=PN，PD⊥MN，MN=2cm，
∴MD=ND= MN=1cm，
∴ON=OD+DN=4+1=5cm．
所以答案是：5．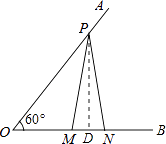
【考点精析】本题主要考查了等腰三角形的性质和含30度角的直角三角形的相关知识点，需要掌握等腰三角形的两个底角相等（简称：等边对等角）；在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半才能正确解答此题．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】为了调查居民的生活水平，有关部门对某居委会的50户居民的家庭存款额进行了调查，数据（单位：万元）如下：
1.7 3.5 2.3 6.4 2.0 1.9 6.7 4.8 5.0 4.7
2.3 3.4 5.6 3.7 2.2 3.3 5.8 4.3 3.6 3.8
3.0 5.1 7.0 3.1 2.9 4.9 5.8 3.6 3.0 4.2
4.0 3.9 5.1 6.3 1.8 3.2 5.1 5.7 3.9 3.1
2.5 2.8 4.5 4.9 5.3 2.6 7.2 1.9 5.0 3.8
（1）这50个家庭存款额的最大值、最小值分别是多少？它们相差多少？
（2）填表：
存款额x（万元） | 划记 | 户数 |
1.0≤x＜2.0 |
| |
2.0≤x＜3.0 |
| |
3.0≤x＜4.0 |
| |
4.0≤x＜5.0 |
| |
5.0≤x＜6.0 |
| |
6.0≤x＜7.0 |
| |
7.0≤x＜8.0 |
|
（3）根据上表谈谈这50户家庭存款额的分布情况．
