题目内容
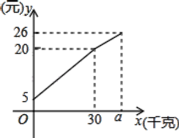
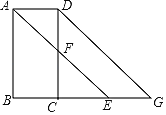
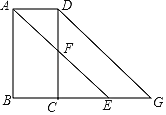
【题目】如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,DG交BC的,延长线于G,∠CFE=∠AEB
(1)若∠B=87°,求∠DCG的度数;
(2)AD与BC是什么位置关系?并说明理由;
(3)若∠DAB=α,∠DGC=β,直接写出α、β满足什么数量关系时,AE∥DG.
【答案】(1)∠DCG=87°;(2)AD∥BC,理由见解析;(3)当α=2β时,AE∥DG.理由见解析.
【解析】
(1)根据平行线的判定定理得到AB∥CD,由平行线的性质得到∠DCG=∠B=87°;
(2)由平行线的性质得到∠BAF=∠CFE,根据角平分线的定义得到∠BAF=∠FAD,等量代换得到∠DAF=∠CFE,∠DAF=∠AEB,由平行线的判定即可得到结论;
(3)根据平行线的判定定理得到∠DAF=∠AEB,根据角平分线的定义得到∠DAB=2∠DAF=2∠AEB,然后根据平行线的性质即可得到结论.
(1)∵∠BAD+∠ADC=180°,
∴AB∥CD,
∴∠DCG=∠B=87°;
(2)AD∥BC,理由如下:
∵AB∥CD,
∴∠BAF=∠CFE,
又∵AE平分∠BAD,
∴∠BAF=∠FAD,
∴∠DAF=∠CFE,
而∠CFE=∠AEB,
∴∠DAF=∠AEB,
∴AD∥BC;
(3)当α=2β时,AE∥DG.理由:
若AE∥DG,则∠G=∠AEB=∠DAE=![]() ∠BAD,
∠BAD,
即当∠BAD=2∠G时,AE∥DG.

练习册系列答案
相关题目