题目内容
【题目】已知,在![]() 中,
中,![]() ,
,![]() 为
为![]() 上一动点,以
上一动点,以![]() 为斜边作
为斜边作![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,且
,且![]() .
.
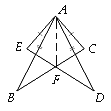
(1)如图①,若![]() 平分
平分![]() ,
,![]() ,求
,求![]() 的长
的长
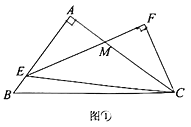
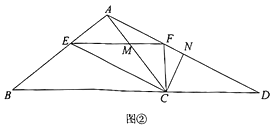
(2)如图②,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,求证
,求证![]() .
.
【答案】(1)12;(2)见解析
【解析】
(1)由“SAS”可证△AEM≌△FCM,可得EM=MC,由等腰三角形性质可求∠AEF=∠MCE=∠MEC=30°,由直角三角形的性质可求ME=MC=8,即可求AC的长;
(2)过点C作CG⊥AC交AD于点G,由“SAS”可证△ACG≌△EFC,可得AG=CE,CF=CG,由等腰三角形的性质可得FG=2FN,即可得结论.
(1)∵EF平分∠AEC,
∴∠AEF=∠FEC,
∵∠BAC=∠EFC=90°,AM=MF,∠AME=∠FMC
∴△AEM≌△FCM(SAS)
∴EM=MC
∴∠MEC=∠MCE
∴∠MEC=∠MCE=∠AEF,
∵∠MEC+∠MCE+∠AEF=90°
∴∠AEF=∠MCE=∠MEC=30°,且∠BAC=90°
∴EM=2AM=8
∴MC=8
∴AC=AM+MC=12
(2)如图,过点C作CG⊥AC交AD于点G,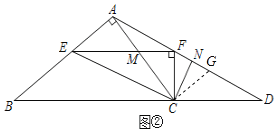
由(1)可知:EM=MC
∵AM=MF
∴AC=EF,
∵∠BAC=∠EFC=90°
∴点A,点F,点C,点E四点共圆
∴∠CAG=∠FEC,且AC=EF,∠EFC=∠ACG=90°
∴△ACG≌△EFC(ASA)
∴AG=CE,CF=CG,
∵CF=CG,CN⊥AG
∴FG=2FN
∴EC=AG=AF+FG=AF+2FN

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目