题目内容
已知P为⊙O内一点，且OP=2cm，如果⊙O的半径是3cm，那么过点P的最长的弦长为分析：过点P最长的弦就是过点P的直径，过点P最短的弦就是过P点与OP垂直的弦，利用勾股定理可以求出最短的弦．
解答：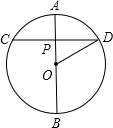
解：如图，AB是过点P最长的弦，是圆的一条直径，
所以AB=6cm．CD是过点P最短的弦，CD⊥OP，
在Rt△OPD中，PD2=OD2-OP2=9-4=5，
∴PD=
，CD=2
．
所以对短的弦长为2
cm．
故答案是：6cm，2
cm．
解：如图，AB是过点P最长的弦，是圆的一条直径，所以AB=6cm．CD是过点P最短的弦，CD⊥OP，
在Rt△OPD中，PD2=OD2-OP2=9-4=5，
∴PD=
| 5 |
| 5 |
所以对短的弦长为2
| 5 |
故答案是：6cm，2
| 5 |
点评：本题考查的是垂径定理，过圆内一点最长的弦是过这点的直径，最短的弦是过这点垂直于OP的弦，利用勾股定理可以求出最短的弦长．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
如图，已知P为△ABC内一点，过P点分别作直线平行于△ABC的各边，形成小三角形的面积S1、S2、S3分别为4、9、16，则△ABC的面积为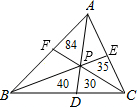
如图所示．已知P为△ABC内一点，AP，BP，CP分别与对边交于D，E，F，把△ABC分成六个小三角形，其中四个小三角形的面积已在图中给出．求△ABC的面积．
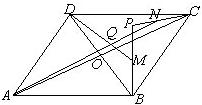17、已知P为?ABCD内一点，O为AC与BD的交点，M、N分别为PB，PC的中点，Q为AN与DM的交点，
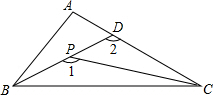如图，已知P为△ABC内一点，BP的延长线交AC于点D，若∠1=（9m-5）°，∠2=（8m+6）°，∠A=（9m-7）°，试求整数m的值．