题目内容
如图，已知P为△ABC内一点，过P点分别作直线平行于△ABC的各边，形成小三角形的面积S1、S2、S3分别为4、9、16，则△ABC的面积为分析：由题意证明S1、S2两个三角形相似对应边得比DP：PE=
=2：3，则DP：DE=2：5，△DPG∽△ADE，能求出△ADE的面积为25，同理可求DE：HF=5：4，可以求出DE：BC的值为5：9，则△ABC的面积就能求出来了．
|
解答：解：由已知可得∠GDE=∠KPE，∠GPD=∠KEP，
∴△GDP∽△KPE，
∴DP：PE=
=2：3，
∴DP：DE=2：5，
由题意可知△DGP∽△DAE，
∴S△DGP：S△DAE=DP2：DE2=4：25，
∴S△DAE=25，
∴S四边形AGPK=S△DAE-S1-S2=12，
同理可得DE：HF=5：4，
∴DE：BC=（2+3）：（2+4+3）=5：9，
∴S△DAE：S△ABC=25：81，
∴△ABC的面积=81．
∴△GDP∽△KPE，
∴DP：PE=
|
∴DP：DE=2：5，
由题意可知△DGP∽△DAE，
∴S△DGP：S△DAE=DP2：DE2=4：25，
∴S△DAE=25，
∴S四边形AGPK=S△DAE-S1-S2=12，
同理可得DE：HF=5：4，
∴DE：BC=（2+3）：（2+4+3）=5：9，
∴S△DAE：S△ABC=25：81，
∴△ABC的面积=81．
点评：本题考查的是灵活运用相似三角形的性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3、如图，已知⊙O，AB为直径，AB⊥CD，垂足为E，由图你还能知道哪些正确的结论请把它们一一写出来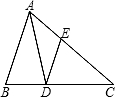
如图，已知AD为△ABC的角平分线，DE∥AB，如果
（2011•成华区二模）如图，已知半径为R的⊙O1的直径AB和弦CD交于点M，点A为
（2012•苏州）如图，已知半径为2的⊙O与直线l相切于点A，点P是直径AB左侧半圆上的动点，过点P作直线l的垂线，垂足为C，PC与⊙O交于点D，连接PA、PB，设PC的长为x（2＜x＜4）．