题目内容
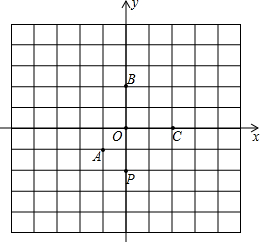（2013•抚顺）如图，在平面直角坐标系中，点A、B、C的坐标分别是（-1，-1）、（0，2）、（2，0），点P在y轴上，且坐标为（0，-2）．点P关于点A的对称点为P1，点P1关于点B的对称点为P2，点P2关于点C的对称点为P3，点P3关于点A的对称点为P4，点P4关于点B的对称点为P5，点P5关于点C的对称点为P6，点P6关于点A的对称点为P7…，按此规律进行下去，则点P2013的坐标、是（2，-4）
（2，-4）
．分析：根据对称依次作出对称点，便不难发现，点P6与点P重合，也就是每6次对称为一个循环组循环，用2013除以6，根据商和余数的情况确定点P2013的位置，然后写出坐标即可．
解答：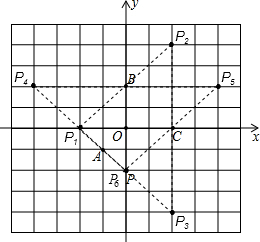
解：如图所示，点P6与点P重合，
∵2013÷6=335…3，
∴点P2013是第336循环组的第3个点，与点P3重合，
∴点P2013的坐标为（2，-4）．
故答案为：（2，-4）．
解：如图所示，点P6与点P重合，∵2013÷6=335…3，
∴点P2013是第336循环组的第3个点，与点P3重合，
∴点P2013的坐标为（2，-4）．
故答案为：（2，-4）．
点评：本题是对点的变化规律的考查，作出图形，观察出每6次对称为一个循环组循环是解题的关键，也是本题的难点．
练习册系列答案
阅读快车系列答案
相关题目
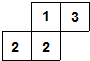（2013•抚顺）如图是由八个小正方形搭成的几何体的俯视图，小正方形中的数字表示该位置上的小正方体的个数，则这个几何体的左视图是（ ）
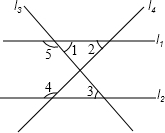（2013•抚顺）如图，直线l1、l2被直线l3、l4所截，下列条件中，不能判断直线l1∥l2的是（ ）
（2013•抚顺）如图，在△ABC中，AB=BC，以AB为直径的⊙O交AC于点D，DE⊥BC，垂足为E．