题目内容
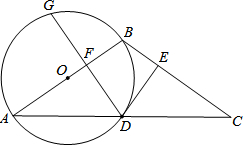（2013•抚顺）如图，在△ABC中，AB=BC，以AB为直径的⊙O交AC于点D，DE⊥BC，垂足为E．（1）求证：DE是⊙O的切线；
（2）若DG⊥AB，垂足为点F，交⊙O于点G，∠A=35°，⊙O半径为5，求劣弧DG的长．（结果保留π）
分析：（1）连接BD，OD，求出OD∥BC，推出OD⊥DE，根据切线判定推出即可；
（2）求出∠BOD=∠GOB，求出∠BOD的度数，根据弧长公式求出即可．
（2）求出∠BOD=∠GOB，求出∠BOD的度数，根据弧长公式求出即可．
解答：（1）证明：连接BD、OD，
∵AB是⊙O直径，
∴∠ADB=90°，
∴BD⊥AC，
∵AB=BC，
∴AD=DC，
∵AO=OB，
∴DO∥BC，
∵DE⊥BC，
∴DE⊥OD，
∵OD为半径，
∴DE是⊙O切线；
（2）解：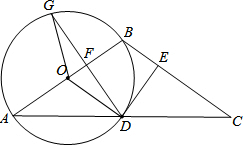
∵DG⊥AB，OB过圆心O，
∴弧BG=弧BD，
∵∠A=35°，
∴∠BOD=2∠A=70°，
∴∠BOG=∠BOD=70°，
∴∠GOD=140°，
∴劣弧DG的长是
=
π．
∵AB是⊙O直径，
∴∠ADB=90°，
∴BD⊥AC，
∵AB=BC，
∴AD=DC，
∵AO=OB，
∴DO∥BC，
∵DE⊥BC，
∴DE⊥OD，
∵OD为半径，
∴DE是⊙O切线；
（2）解：
∵DG⊥AB，OB过圆心O，∴弧BG=弧BD，
∵∠A=35°，
∴∠BOD=2∠A=70°，
∴∠BOG=∠BOD=70°，
∴∠GOD=140°，
∴劣弧DG的长是
| 140π×5 |
| 180 |
| 35 |
| 9 |
点评：本题考查了弧长公式，切线的判定，平行线性质和判定，圆周角定理，等腰三角形的性质和判定，三角形的中位线等知识点的应用，主要考查学生综合运用定理进行推理和计算的能力．
练习册系列答案
目标测试系列答案
相关题目
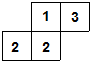（2013•抚顺）如图是由八个小正方形搭成的几何体的俯视图，小正方形中的数字表示该位置上的小正方体的个数，则这个几何体的左视图是（ ）
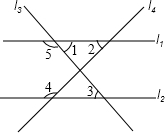（2013•抚顺）如图，直线l1、l2被直线l3、l4所截，下列条件中，不能判断直线l1∥l2的是（ ）
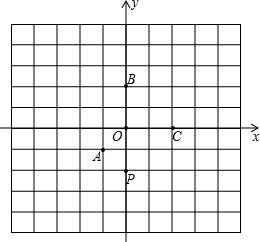（2013•抚顺）如图，在平面直角坐标系中，点A、B、C的坐标分别是（-1，-1）、（0，2）、（2，0），点P在y轴上，且坐标为（0，-2）．点P关于点A的对称点为P1，点P1关于点B的对称点为P2，点P2关于点C的对称点为P3，点P3关于点A的对称点为P4，点P4关于点B的对称点为P5，点P5关于点C的对称点为P6，点P6关于点A的对称点为P7…，按此规律进行下去，则点P2013的坐标、是