题目内容
【题目】(8分)已知AB是⊙O的直径,C是圆周上的动点,P是优弧![]() 中点.
中点.
(1)求证:OP∥BC.
(2)连接PC交直径AB于点D,当OC=DC时,求∠A的度数.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接AC,延长PO交AC于H,根据垂径定理OH ![]() ,∠ACB=90°,所以OP∥BC得证.
,∠ACB=90°,所以OP∥BC得证.
(2) 设∠OPC=x,利用圆中两条半径特有的等腰三角形,同弧所对圆周角是圆心角的一半,用x表示△COD内角和,求出x.
(1)证明:连接AC,延长PO交AC于H,如图1,

∵P是优弧![]() 的中点, ∴PH⊥AC,
的中点, ∴PH⊥AC,
∵AB是⊙O的直径, ∴∠ACB=90°,
∴BC⊥AC, ∴OP∥BC;
(2)连接AC,延长PO交AC于H,如图2,
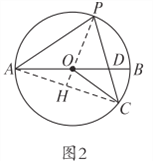
∵P是优弧![]() 的中点, ∴PA=PC, ∴∠PAC=∠PCA,
的中点, ∴PA=PC, ∴∠PAC=∠PCA,
∵OA=OC, ∴∠OAC=∠OCA, ∴∠PAO=PCO,
当CO=CD时,设∠DCO=x,
则∠OPC=x,∠PAO=x, ∴∠PDO=2x,
∴∠ODC=∠POD+∠OPC=3x,
∵CD=CO, ∴∠DOC=∠ODC=3x.
在△POC中,x+x+5x=180°,
解得x=![]() ,即∠PAO=
,即∠PAO=![]() ,∴∠A的度数为
,∴∠A的度数为![]() .
.

练习册系列答案
相关题目
