题目内容
【题目】在△ABC中,AB=2,AC=![]() ,∠B=30°.求∠BAC的度数.
,∠B=30°.求∠BAC的度数.
【答案】∠BAC的度数为105°或15°.
【解析】试题分析:本题考查解直角三角形,由于题目没有给出△ABC的形状,所以要将∠BAC分为钝角和锐角进行分类分析,可过点A作AD⊥BC,在Rt△ADB中,结合已知的条件可求出∠BAD和AD, 在Rt△ADC中,结合已知条件AD和AC,利用锐角三角函数可求出∠CAD,再结合图形求出∠BAC.
解:(1)如图①,当∠BAC是钝角时,过点A作AD⊥BC,垂足为点D.在Rt△ABD中,∵∠B=30°,
∴∠BAD=60°,AD=AB·sin 30°=1.
在Rt△ACD中,CD=![]() =
=![]() =1,
=1,
∴△ACD是等腰直角三角形,则∠CAD=45°,
∴∠BAC=∠BAD+∠CAD=60°+45°=105°.
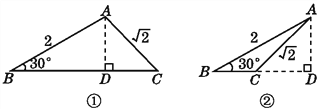
(2)如图②,当∠BAC是锐角时,过点A作AD⊥BC,交BC的延长线于点D.
∵∠B=30°,∴AD=AB·sin 30°=1,∠BAD=60°.
∴CD=![]() =
=![]() =1,
=1,
∴∠DAC=45°,
∴∠BAC=∠BAD-∠DAC=60°-45°=15°.
综上可知,∠BAC的度数为105°或15°.
常见错解:解题时只考虑了一种情况(∠BAC为钝角或∠BAC为锐角),而忽略了另一种情况(∠BAC为锐角或∠BAC为钝角),从而造成漏解.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
【题目】某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:
部门 | 人数 | 每人创年利润(万元) |
A | 1 | 10 |
B | 3 | 8 |
C | 7 | 5 |
D | 4 | 3 |
这15名员工每人所创年利润的众数、中位数分别是( )
A.10,5
B.7,8
C.5,6.5
D.5,5


