题目内容
(2002•泉州)已知:直线l的解析式为y= x+m(m为常数,m≠0),点(-4,3)在直线l上.
x+m(m为常数,m≠0),点(-4,3)在直线l上.(1)求m的值;
(2)若⊙A的圆心为原点,半径为R,并且⊙A与直线l有公共点,试求R的取值范围;
(3)当(2)中的⊙A与l有唯一公共点时,将此时的⊙A向左移动(圆心始终保持在x轴上),试求在这个移动过程中,当直线l被⊙A截得的弦的长为
 时圆心A的坐标.
时圆心A的坐标.
【答案】分析:(1)可将点(-4,3)代入直线l的解析式中,求出m的值.
(2)⊙A与直线l有公共点,则圆与直线l相交或相切,求此时R的取值范围,就必须求出圆心到直线l的距离.过A作AD⊥直线l与D,设直线交x轴于B,交y轴于C,有直线l的解析式,可得出B,C的坐标,那么就有了OB,OC的长,根据勾股定理就能求出BC的长,根据直角三角形ABC的面积的不同的表示方法,可求出AD的长,即圆心到直线L的距离,然后根据圆与直线相交或相切,则圆的半径≥圆到直线的距离.
(3)可过A作直线L的垂线,有被截得弦的长度,有圆的半径,那么圆心到直线的距离就能求出来了,然后根据直线l与x轴的夹角的正弦值,用圆到直线的距离求出AB的长,然后根据B点的坐标即AB的长,求出A到原点的距离,从而求出A的坐标.
解答:解:(1)根据题意,得:3= (-4)+m,解得:m=6.
(-4)+m,解得:m=6.

(2)直线l的解析式为y= x+6,如图(1),设直线l分别于x轴,y轴交于B,C两点.
x+6,如图(1),设直线l分别于x轴,y轴交于B,C两点.
令x=0,得y=6;令y=0,得x=-8.
∴B,C坐标分别为B(-8,0),C(0,6).即AB=8,AC=6.
在直角三角形ABC中,BC= =10.
=10.
过点A作AD⊥BC于D.
∵ AD•BC=
AD•BC= AC•BD,
AC•BD,
∴AD= .
.
又直线l与⊙A有公共点,即l与OA相切或相交,
∴R≥ .
.

(3)当(2)中⊙A与l有惟一公共点时,⊙A与l相切,
∴R= .
.
将该圆向左移动直线l被⊙A截得的弦的长为 时,设截得的弦为DE,那么DE=
时,设截得的弦为DE,那么DE= ,
,
过A作AF⊥DE于F,根据垂径定理EF=DF= ,
,
直角三角形AFE中,AE=R= ,AF=
,AF= =4.
=4.
直角三角形CDO中,tan∠CBO= =
= ,因此sin∠CBO=
,因此sin∠CBO= .
.
直角三角形FBA中,AF=4,sin∠CBO= .AB=AF÷sin∠CBO=
.AB=AF÷sin∠CBO= .
.
因此,OA=OB-AB=8-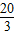 =
= ,
,
当A在B的左侧时,BA′=BA=8- ,
,
即OA′=8+(8- )=14
)=14 ,
,
因此A点的坐标是( ,0)或(-14
,0)或(-14 ,0).
,0).
点评:本题结合了一次函数考查了直线与圆的位置关系,本题中根据直线的函数求出直线与坐标轴的交点,然后根据交点的坐标得出线段的长进而求出圆心到直线的距离是解题的关键.
(2)⊙A与直线l有公共点,则圆与直线l相交或相切,求此时R的取值范围,就必须求出圆心到直线l的距离.过A作AD⊥直线l与D,设直线交x轴于B,交y轴于C,有直线l的解析式,可得出B,C的坐标,那么就有了OB,OC的长,根据勾股定理就能求出BC的长,根据直角三角形ABC的面积的不同的表示方法,可求出AD的长,即圆心到直线L的距离,然后根据圆与直线相交或相切,则圆的半径≥圆到直线的距离.
(3)可过A作直线L的垂线,有被截得弦的长度,有圆的半径,那么圆心到直线的距离就能求出来了,然后根据直线l与x轴的夹角的正弦值,用圆到直线的距离求出AB的长,然后根据B点的坐标即AB的长,求出A到原点的距离,从而求出A的坐标.
解答:解:(1)根据题意,得:3=
 (-4)+m,解得:m=6.
(-4)+m,解得:m=6.
(2)直线l的解析式为y=
 x+6,如图(1),设直线l分别于x轴,y轴交于B,C两点.
x+6,如图(1),设直线l分别于x轴,y轴交于B,C两点.令x=0,得y=6;令y=0,得x=-8.
∴B,C坐标分别为B(-8,0),C(0,6).即AB=8,AC=6.
在直角三角形ABC中,BC=
 =10.
=10.过点A作AD⊥BC于D.
∵
 AD•BC=
AD•BC= AC•BD,
AC•BD,∴AD=
 .
.又直线l与⊙A有公共点,即l与OA相切或相交,
∴R≥
 .
.
(3)当(2)中⊙A与l有惟一公共点时,⊙A与l相切,
∴R=
 .
.将该圆向左移动直线l被⊙A截得的弦的长为
 时,设截得的弦为DE,那么DE=
时,设截得的弦为DE,那么DE= ,
,过A作AF⊥DE于F,根据垂径定理EF=DF=
 ,
,直角三角形AFE中,AE=R=
 ,AF=
,AF= =4.
=4.直角三角形CDO中,tan∠CBO=
 =
= ,因此sin∠CBO=
,因此sin∠CBO= .
.直角三角形FBA中,AF=4,sin∠CBO=
 .AB=AF÷sin∠CBO=
.AB=AF÷sin∠CBO= .
.因此,OA=OB-AB=8-
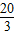 =
= ,
,当A在B的左侧时,BA′=BA=8-
 ,
,即OA′=8+(8-
 )=14
)=14 ,
,因此A点的坐标是(
 ,0)或(-14
,0)或(-14 ,0).
,0).点评:本题结合了一次函数考查了直线与圆的位置关系,本题中根据直线的函数求出直线与坐标轴的交点,然后根据交点的坐标得出线段的长进而求出圆心到直线的距离是解题的关键.

练习册系列答案
相关题目

 x+m(m为常数,m≠0),点(-4,3)在直线l上.
x+m(m为常数,m≠0),点(-4,3)在直线l上. 时圆心A的坐标.
时圆心A的坐标.