题目内容
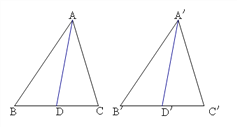
【题目】如图,△ABC≌△A'B'C',AD、A'D'分别是△ABC、△A'B'C'的对应边上的中线,判断AD与A'D'有怎样的数量关系?证明你的结论.
【答案】AD=A'D',证明见解析.
【解析】试题分析:先由全等三角形的性质得出AB=A'B',BC=B'C',∠B=∠B',再 由中线的性质得出BD=B'D',最后由SAS证出△ABD≌△A'B'D',即可得出AD=A'D'.
试题解析:AD=A'D',证明如下:
证明: ∵△ABC≌△A'B'C',
∴AB=A'B',BC=B'C',∠B=∠B',
∵AD、A'D'分别是BC与B'C'边上的中线,
∴BD=B'D',
在△ABD和△A'B'D'中,
 ,
,
∴△ABD≌△A'B'D'(SAS),
∴ AD=A'D'.

练习册系列答案
相关题目

