题目内容
【题目】已知:点A(﹣1,0),B(0,﹣3). 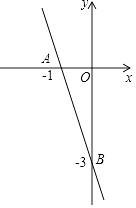
(1)求:直线AB的表达式;
(2)直接写出直线AB向下平移2个单位后得到的直线表达式;
(3)求:在(2)的平移中直线AB在第三象限内扫过的图形面积.
【答案】
(1)解:设直线AB的表达式为y=kx+b,
将A(﹣1,0)、B(0,﹣3)代入y=kx+b,
![]() ,解得:
,解得: ![]() ,
,
∴直线AB的表达式为y=﹣3x﹣3
(2)解:根据平移的性质可知:直线AB:y=﹣3x﹣3向下平移2个单位后得到的直线表达式为y=﹣3x﹣3﹣2=﹣3x﹣5
(3)解:设直线y=﹣3x﹣5与x轴交点为点D,与y轴的交点为点C,
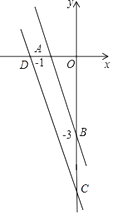
在y=﹣3x﹣5中,当x=0时,y=﹣5,
∴点C的坐标为(0,﹣5);
当y=﹣3x﹣5时,x=﹣ ![]() ,
,
∴点D的坐标为(﹣ ![]() ,0).
,0).
∴直线AB在第三象限内扫过的图形面积=S△DOC﹣S△AOB= ![]() ×
× ![]() ×5﹣
×5﹣ ![]() ×1×3=
×1×3= ![]() .
.
【解析】(1)根据点A、B的坐标利用待定系数法即可求出直线AB的表达式;(2)根据平移的性质“上加下减,左加右减”即可得出平移后的直线表达式;(3)设直线y=﹣3x﹣5与x轴交点为点D,与y轴的交点为点C,根据一次函数图象上点的坐标特征可求出点C、D的坐标,再根据直线AB在第三象限内扫过的图形面积=S△DOC﹣S△AOB结合三角形的面积公式即可得出结论.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目