题目内容
【题目】我们知道:等腰三角形两腰上的高相等.

(1)请你写出它的逆命题:______.
(2)逆命题是真命题吗?若是,请证明;若不是,请举出反例(要求:画出图形,写出已知,求证和证明过程).
【答案】(1)两边上的高相等的三角形是等腰三角形;(2)是,证明见解析.
【解析】
(1)根据逆命题的定义即可写出结论;
(2)根据题意,写出已知和求证,然后利用HL证出Rt△BCD≌Rt△CBE,从而得出∠ABC=∠ACB,然后根据等角对等边即可证出结论.
(1)等腰三角形两腰上的高相等的逆命题是两边上的高相等的三角形是等腰三角形,
故答案为:两边上的高相等的三角形是等腰三角形;
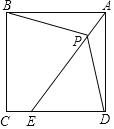
(2)如图,已知CD和BE是AB和AC边上的高,CD=BE,
求证:AB=AC;
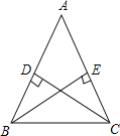
证明:如图,在△ABC中,BE⊥AC,CD⊥AB,且BE=CD.
∵BE⊥AC,CD⊥AB,
∴∠CDB=∠BEC=90°,
在Rt△BCD与Rt△CBE中,
![]() ,
,
∴Rt△BCD≌Rt△CBE(HL),
∴∠ABC=∠ACB,
∴AB=AC,即△ABC是等腰三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目