题目内容
如图,将一副三角板拼在一起得到四边形ABCD,E为CD的中点,AB=c,将△ADE沿直线AE翻折得△AD′E,则点D′到AB边的距离为 .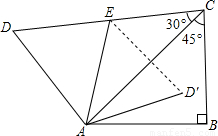
【答案】分析:过D′作D′F⊥AB于F点,由△ABC是等腰直角三角形,得AC=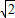 AB=
AB=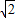 c;由△ADC是含30°的直角三角形,得到AD=
c;由△ADC是含30°的直角三角形,得到AD=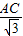 =
=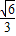 c;又根据斜边上的中线等于斜边的一半得到EA=ED=EC,于是有∠D=∠EAD=60°,∠EAC=∠ECA=30°,根据折叠的性质得到AD′=AD=
c;又根据斜边上的中线等于斜边的一半得到EA=ED=EC,于是有∠D=∠EAD=60°,∠EAC=∠ECA=30°,根据折叠的性质得到AD′=AD=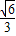 c,∠EAD′=60′,得到∠CAD′=30°,则∠D′AF=15°,由sin∠D′AF=sin15°=
c,∠EAD′=60′,得到∠CAD′=30°,则∠D′AF=15°,由sin∠D′AF=sin15°=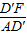 =
=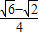 ,即可得到D′F的长.
,即可得到D′F的长.
解答: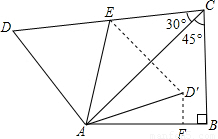 解:过D′作D′F⊥AB于F点,如图,
解:过D′作D′F⊥AB于F点,如图,
∵△ABC是等腰直角三角形,
∴AC=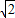 AB=
AB=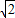 c;
c;
又∵△ADC是含30°的直角三角形,
∴AD=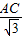 =
=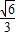 c,
c,
∵E为CD的中点,
∴EA=ED=EC,
∴∠D=∠EAD=60°,∠EAC=∠ECA=30°,
而△ADE沿直线AE翻折得△AD′E,
∴AD′=AD=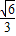 c,∠EAD′=60′,
c,∠EAD′=60′,
∴∠CAD′=60°-30°=30°,
∴∠D′AF=45°-30°=15°,
(如图,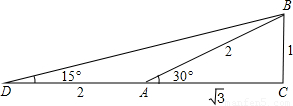 DB=
DB=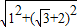 =
=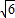 +
+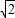 ,sin15°=
,sin15°=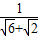 =
=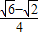 ),
),
∴sin∠D′AF=sin15°=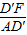 =
=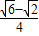 ,
,
∴D′F=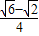 •
• c=
c=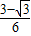 c.
c.
即点D′到AB边的距离为 c.
c.
故答案为: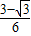 c.
c.
点评:本题考查了折叠的性质:折叠后得到的图形和原图形全等.也考查了等腰直角三角形和含30度的直角三角形的三边关系以及15度的三角函数值.
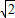 AB=
AB=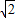 c;由△ADC是含30°的直角三角形,得到AD=
c;由△ADC是含30°的直角三角形,得到AD=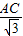 =
=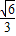 c;又根据斜边上的中线等于斜边的一半得到EA=ED=EC,于是有∠D=∠EAD=60°,∠EAC=∠ECA=30°,根据折叠的性质得到AD′=AD=
c;又根据斜边上的中线等于斜边的一半得到EA=ED=EC,于是有∠D=∠EAD=60°,∠EAC=∠ECA=30°,根据折叠的性质得到AD′=AD=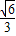 c,∠EAD′=60′,得到∠CAD′=30°,则∠D′AF=15°,由sin∠D′AF=sin15°=
c,∠EAD′=60′,得到∠CAD′=30°,则∠D′AF=15°,由sin∠D′AF=sin15°=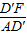 =
=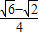 ,即可得到D′F的长.
,即可得到D′F的长.解答:
 解:过D′作D′F⊥AB于F点,如图,
解:过D′作D′F⊥AB于F点,如图,∵△ABC是等腰直角三角形,
∴AC=
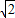 AB=
AB=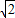 c;
c;又∵△ADC是含30°的直角三角形,
∴AD=
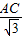 =
=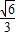 c,
c,∵E为CD的中点,
∴EA=ED=EC,
∴∠D=∠EAD=60°,∠EAC=∠ECA=30°,
而△ADE沿直线AE翻折得△AD′E,
∴AD′=AD=
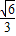 c,∠EAD′=60′,
c,∠EAD′=60′,∴∠CAD′=60°-30°=30°,
∴∠D′AF=45°-30°=15°,
(如图,
 DB=
DB=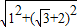 =
=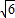 +
+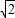 ,sin15°=
,sin15°=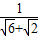 =
=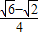 ),
),∴sin∠D′AF=sin15°=
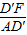 =
=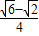 ,
,∴D′F=
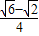 •
• c=
c=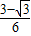 c.
c.即点D′到AB边的距离为
 c.
c.故答案为:
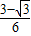 c.
c.点评:本题考查了折叠的性质:折叠后得到的图形和原图形全等.也考查了等腰直角三角形和含30度的直角三角形的三边关系以及15度的三角函数值.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
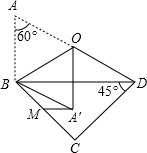 如图,一副三角板拼在一起,O为AD的中点,AB=a.将△ABO沿BO对折于△A′BO,M为BC上一动点,则A′M的最小值为
如图,一副三角板拼在一起,O为AD的中点,AB=a.将△ABO沿BO对折于△A′BO,M为BC上一动点,则A′M的最小值为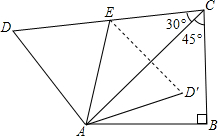 如图,将一副三角板拼在一起得到四边形ABCD,E为CD的中点,AB=c,将△ADE沿直线AE翻折得△AD′E,则点D′到AB边的距离为
如图,将一副三角板拼在一起得到四边形ABCD,E为CD的中点,AB=c,将△ADE沿直线AE翻折得△AD′E,则点D′到AB边的距离为
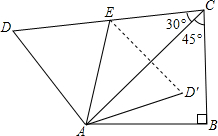 如图,将一副三角板拼在一起得到四边形ABCD,E为CD的中点,AB=c,将△ADE沿直线AE翻折得△AD′E,则点D′到AB边的距离为________.
如图,将一副三角板拼在一起得到四边形ABCD,E为CD的中点,AB=c,将△ADE沿直线AE翻折得△AD′E,则点D′到AB边的距离为________.