Question

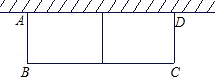如图所示，某农户想建造一花圃，用来种植两种不同的花卉，以供应城镇市场需要，现用长为36m的篱笆，一面砌墙（墙的最大可使用长度l=13m），围成中间隔有一道篱笆的长方形花圃，设花圃宽AB为x，面积为S．
（1）求S与x的函数关系式．
（2）若要围成面积为96m²的花圃，求宽AB的长度．
（3）花圃的面积能达到108m²吗？若能，请求出AB的长度，若不能请说明理由．

Answer 1

解：（1）设花圃宽AB为x，面积为S．
则S=（36-3x）x=-3x²+36x；

（2）设AB的长是x米．
（36-3x）x=96，
解得x₁=4，x₂=8，
当x=4时，长方形花圃的长为36-3x=24，又墙的最大可用长度a是13m，故舍去；
当x=8时，长方形花圃的长为24-3x=12，符合题意；
∴AB的长为8m．

（3）花圃的面积为S=（36-3x）x=-3（x-6）²+108，
∴当AB长为6m，宽为16m时，有最大面积，为108平方米．
又∵当AB=6m时，长方形花圃的长为36-3×4=24，又墙的最大可用长度a是13m，故舍去；
故花圃的面积不能达到108m²．
分析：（1）等量关系为：（篱笆长-3AB）×AB=S，即可得出答案；
（2）等量关系为：（篱笆长-3AB）×AB=96，把相关数值代入求得合适的解即可；
（3）把（1）中用代数式表示的面积整理为a（x-h）²+b的形式可得最大的面积．
点评：本题考查了一元二次方程及配方法的应用；得到长方形花圃的长的代数式是解决本题的易错点；用配方法得到最大面积是解决本题的难点．