题目内容
已知方程x2-px+4=0(1)与2x2-9x+q=0(2).若方程(2)的一个根比方程(1)的较大根大2,方程(2)的另一个根比方程(1)的较小根小2,则q的值为
- A.

- B.

- C.
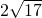
- D.
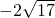
D
分析:由题意可得,方程(1)(2)的两根之和相等,由根与系数的关系可得x1x2、x1+x2的值,因为x3x4=(x1+2)(x2-2)=x1x2+2(x2-x1)-4=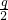 ,将相应数值代入,从而求出q.
,将相应数值代入,从而求出q.
解答:设方程(1)的两根为x1、x2(x1<x2),方程(2)的两根为x3、x4,
由题意得x1+x2=x3+x4,
由根与系数的关系得x1+x2=p,x3+x4=4.5,x1x2=4,x3x4=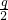 ,
,
∴(x1-x2)2=(x1+x2)2-4x1x2= ,
,
∴x2-x1=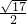 ,
,
∴x3x4=(x1-2)(x2+2)=x1x2+2(x1-x2)-4=- ,
,
∴q=-2 .
.
故选D.
点评:本题考查一元二次方程根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.
分析:由题意可得,方程(1)(2)的两根之和相等,由根与系数的关系可得x1x2、x1+x2的值,因为x3x4=(x1+2)(x2-2)=x1x2+2(x2-x1)-4=
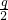 ,将相应数值代入,从而求出q.
,将相应数值代入,从而求出q.解答:设方程(1)的两根为x1、x2(x1<x2),方程(2)的两根为x3、x4,
由题意得x1+x2=x3+x4,
由根与系数的关系得x1+x2=p,x3+x4=4.5,x1x2=4,x3x4=
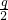 ,
,∴(x1-x2)2=(x1+x2)2-4x1x2=
 ,
,∴x2-x1=
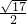 ,
,∴x3x4=(x1-2)(x2+2)=x1x2+2(x1-x2)-4=-
 ,
,∴q=-2
 .
.故选D.
点评:本题考查一元二次方程根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目