题目内容
如图是规格为8×8的正方形网格(网格小正方形的边长为1),请在所给网格中按下列要求操作:(1)请在网格中建立平面直角坐标系,使A点坐标为(-2,3),B点坐标为(-4,1);
(2)在第二象限内的格点上画一点C,使点C与线段AB围成一个直角三角形(不是等腰直角三角形),则C点坐标是______,△ABC的面积是______;
(3)将(2)中画出△ABC以点C为旋转中心,逆时针旋转90°后得△A′B′C.求经过B、C、B′三点的抛物线的解析式;并判断抛物线是否经过8×8正方形网格的格点(不包括点B、C、B′),若经过,请你直接写出点坐标.
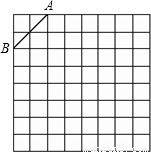
【答案】分析:(1)根据A点坐标为(-2,3),B点坐标为(-4,1),即可作出平面直角坐标系;
(2)由在第二象限内的格点上画一点C,使点C与线段AB围成一个直角三角形(不是等腰直角三角形),根据勾股定理的逆定理即可求得点C坐标,又由直角三角形面积的求解方法,即可求得△ABC的面积;
(3)利用旋转的知识,首先画出△A′B′C,即可求得点C′的坐标,然后利用待定系数法即可求得此二次函数的解析式,继而求得经过8×8正方形网格的格点的坐标.
解答: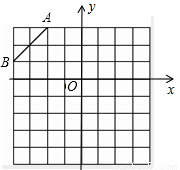 解:(1)∵A点坐标为(-2,3),B点坐标为(-4,1),所以平面直角坐标系如图:(2分)
解:(1)∵A点坐标为(-2,3),B点坐标为(-4,1),所以平面直角坐标系如图:(2分)
(2)∵不是等腰直角三角形,
∴C点坐标是(-1,2),(2分)
∵AB=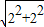 =2
=2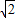 ,AC=
,AC=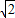 ,BC=
,BC=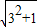 =
=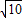 ,
,
即AB2+AC2=BC2,
∴C点坐标是(-1,2);
∴S△ABC= AB•AC=
AB•AC= ×2
×2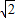 ×
×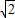 =2;
=2;
故答案为:(-1,2),2;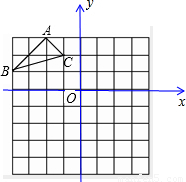
(3)如图:点B′的坐标为(0,-1),
设经过B、C、B′三点的抛物线的解析式为:y=ax2+bx+c,
∴ ,
,
解得: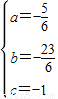 ,
,
∴经过B、C、B′三点的抛物线的解析式为y=- x2-
x2-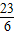 x-1 (3分)(图1分)
x-1 (3分)(图1分)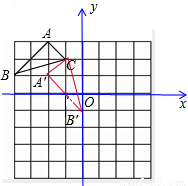
经过,点为:(-3,3).--(1分)
点评:此题考查了平面直角坐标系的确定,直角三角形的判定与性质,旋转的知识以及待定系数法求二次函数解析式等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想的应用.
(2)由在第二象限内的格点上画一点C,使点C与线段AB围成一个直角三角形(不是等腰直角三角形),根据勾股定理的逆定理即可求得点C坐标,又由直角三角形面积的求解方法,即可求得△ABC的面积;
(3)利用旋转的知识,首先画出△A′B′C,即可求得点C′的坐标,然后利用待定系数法即可求得此二次函数的解析式,继而求得经过8×8正方形网格的格点的坐标.
解答:
 解:(1)∵A点坐标为(-2,3),B点坐标为(-4,1),所以平面直角坐标系如图:(2分)
解:(1)∵A点坐标为(-2,3),B点坐标为(-4,1),所以平面直角坐标系如图:(2分)(2)∵不是等腰直角三角形,
∴C点坐标是(-1,2),(2分)
∵AB=
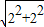 =2
=2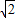 ,AC=
,AC=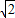 ,BC=
,BC=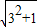 =
=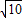 ,
,即AB2+AC2=BC2,
∴C点坐标是(-1,2);
∴S△ABC=
 AB•AC=
AB•AC= ×2
×2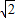 ×
×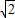 =2;
=2;故答案为:(-1,2),2;

(3)如图:点B′的坐标为(0,-1),
设经过B、C、B′三点的抛物线的解析式为:y=ax2+bx+c,
∴
 ,
,解得:
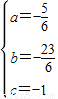 ,
,∴经过B、C、B′三点的抛物线的解析式为y=-
 x2-
x2-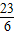 x-1 (3分)(图1分)
x-1 (3分)(图1分)
经过,点为:(-3,3).--(1分)
点评:此题考查了平面直角坐标系的确定,直角三角形的判定与性质,旋转的知识以及待定系数法求二次函数解析式等知识.此题综合性很强,难度较大,解题的关键是注意数形结合思想的应用.

练习册系列答案
相关题目
 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作: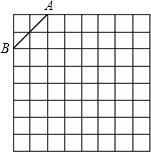 操作:
操作: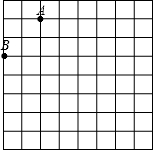 如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作: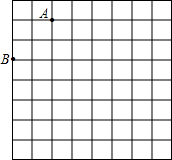 如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是
如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);在第二象限内的格点上找点C(C点的横坐标大于-3),使点C与线段AB组成一个以AB为底的等腰三角形,则C点坐标是