题目内容
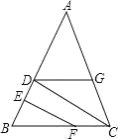
【题目】如图,点P为△ABC的内心,延长AP交△ABC的外接圆于D,在AC延长线上有一点E,满足AD2=ABAE.
求证:DE是⊙O的切线.
【答案】证明:连接DC,DO并延长交⊙O于F,连接AF. 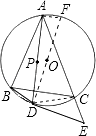
∵P点为△ABC的内心,
∴∠BAD=∠DAE,
又∵AD2=ABAE,即 ![]() =
= ![]() ,
,
∴△BAD∽△DAE,
∴∠ADB=∠E.
又∵∠ADB=∠ACB,
∴∠ACB=∠E,BC∥DE,
∴∠CDE=∠BCD=∠BAD=∠DAC,
又∵∠CAF=∠CDF,
∴∠FDE=∠CDE+∠CDF=∠DAC+∠CAF=∠DAF=90°,
故DE是⊙O的切线.
【解析】连接DC、AF,连接DO并延长交圆O于点F,先证△BAD∽△DAE,得到∠ADB=∠E,再由平行线的性质可证∠FDE=90°可得.解答此题的关键是作出辅助线,证出△BAD∽△DAE.

练习册系列答案
相关题目