题目内容
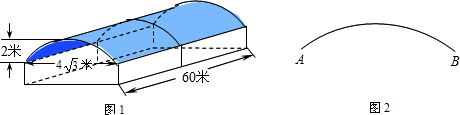
如图1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分;图2是车棚顶部截面的示意图.(1)用尺规在图2中作出弧AB所在圆的圆心(保留作图痕迹,不写作法与证明);
(2)车棚顶部是用一种帆布覆盖的,由图1中给出数据求覆盖棚顶的帆布的面积(不考虑接缝等因素,计算结果保留π).

【答案】分析:(1)根据弦的垂直平分线必过圆心,只需作两条弦的垂直平分线,则交点即为圆心;
(2)覆盖棚顶的帆布的面积等于弧AB的长乘以60,要求弧长,则需求得弧所对的圆心角和半径的长,因此可以构造半径、半弦、弦心距组成的直角三角形,根据勾股定理进行求解.
解答:解:(1)如图所示:
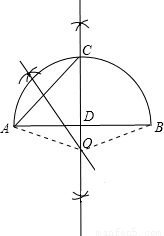 ;
;
(2)如(1)中的图,根据垂径定理,得AD=2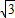 .
.
设圆的半径是r.
在直角三角形AOD中,根据勾股定理,得
r2=(r-2)2+(2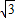 )2,
)2,
解得r=4.
则OD=2.
∴∠AOD=60°,
∴∠AOB=2∠AOD=120°,
则弧AB的长是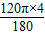 =
=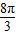 ,
,
则覆盖棚顶的帆布的面积是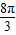 ×60=160π(m2).
×60=160π(m2).
点评:此题考查了垂径定理及其推论的运用,能够根据垂径定理的推论求作一条弧所在圆的圆心,能够构造半径、半弦、弦心距的直角三角形.
(2)覆盖棚顶的帆布的面积等于弧AB的长乘以60,要求弧长,则需求得弧所对的圆心角和半径的长,因此可以构造半径、半弦、弦心距组成的直角三角形,根据勾股定理进行求解.
解答:解:(1)如图所示:
 ;
;(2)如(1)中的图,根据垂径定理,得AD=2
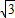 .
.设圆的半径是r.
在直角三角形AOD中,根据勾股定理,得
r2=(r-2)2+(2
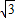 )2,
)2,解得r=4.
则OD=2.
∴∠AOD=60°,
∴∠AOB=2∠AOD=120°,
则弧AB的长是
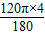 =
=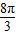 ,
,则覆盖棚顶的帆布的面积是
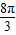 ×60=160π(m2).
×60=160π(m2).点评:此题考查了垂径定理及其推论的运用,能够根据垂径定理的推论求作一条弧所在圆的圆心,能够构造半径、半弦、弦心距的直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目