题目内容
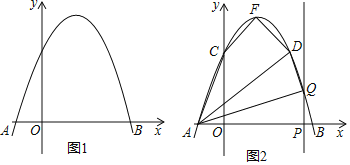
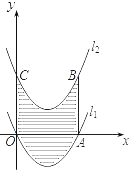
【题目】如图，已知抛物线l1：y＝
（x﹣2）2﹣2与x轴分别交于O、A两点，将抛物线L1向上平移得到L2，过点A作AB⊥x轴交抛物线L2于点B，如果由抛物线L1、L2、直线AB及y轴所围成的阴影部分的面积为16，则抛物线L2的函数表达式为_____．
【答案】y＝
（x﹣2）2+2
【解析】
利用二次函数图象上点的坐标特征求出抛物线与x轴交点的横坐标，由阴影部分的面积等于矩形OABC的面积可求出AB的长度，再利用平移的性质“左加右减，上加下减”，即可求出抛物线L2的函数表达式．
解：当y＝0时，有（x﹣2）2﹣2＝0，
解得：x1＝0，x2＝4，
∴OA＝4．
∵S阴影＝OAAB＝16，
∴AB＝4，
∴抛物线L2的函数表达式为y＝（x﹣2）2﹣2+4＝（x﹣2）2+2．
故答案为：y＝（x﹣2）2+2．
练习册系列答案
相关题目
