Question

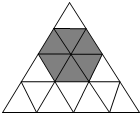向如图所示的正三角形区域内扔沙包，（区域中每个小正三角形陈颜色外完全相同）沙包随机落在某个正三角形内．
（1）扔沙包一次，落在图中阴影区域的概率是

3

8

．
（2）要使沙包落在图中阴影区域和空白区域的概率均为

1

2

，还要涂黑几个小正三角形？请在图中画出．

Answer 1

分析：（1）求出阴影部分的面积与三角形的面积的比值即可解答；
（2）利用（1）中求法得出答案即可．

解答：解：因为阴影部分的面积与三角形的面积的比值是

6

16

=

3

8

，
所以扔沙包1次击中阴影区域的概率等于

3

8

．
故答案为：

3

8

．

（2）如图所示：
要使沙包落在图中阴影区域和空白区域的概率均为

1

2

，
还要涂黑2个小正三角形（答案不唯一）．

点评：本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率．