题目内容
向如图所示的正三角形区域扔沙包（区域中每一个小正三角形除颜色外完全相同），假设沙包击中每一个小三角形是等可能的，扔沙包1次击中阴影区域的概率等于| 3 |
| 8 |
| 3 |
| 8 |
分析：求出阴影部分的面积与三角形的面积的比值即可解答．
解答：解：因为阴影部分的面积与三角形的面积的比值是
=
，
所以扔沙包1次击中阴影区域的概率等于
．
故答案为：
．
| 6 |
| 16 |
| 3 |
| 8 |
所以扔沙包1次击中阴影区域的概率等于
| 3 |
| 8 |
故答案为：
| 3 |
| 8 |
点评：本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
（2012•连云港）向如图所示的正三角形区域扔沙包（区域中每一个小正三角形除颜色外完全相同），假设沙包击中每一个小三角形是等可能的，扔沙包1次击中阴影区域的概率等于（ ）
向如图所示的正三角形区域扔沙包（区域中每一个小正三角形除颜色外完全相同），假设沙包击中每一个小正三角形是等可能的，扔沙包1次，击中阴影区域概率等于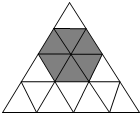
向如图所示的正三角形区域内扔沙包，（区域中每个小正三角形陈颜色外完全相同）沙包随机落在某个正三角形内．