题目内容
已知等腰△ABC的一边a=2,若另两边b、c恰好是关于x的一元二次方程x2-(k+3)x+3k=0的两个根,求△ABC的周长.
分析:先利用因式分解法解一元二次方程x2-(k+3)x+3k=0得到x1=3,x2=k,由于等腰△ABC的三边为a、b、c,则b=c,得到k=3;或b=2,c=3或c=2,b=3,则k=2,然后利用三角形的周长公式计算即可.
解答:解:x2-(k+3)x+3k=0
(x-3)(x-k)=0,
则x1=3,x2=k,
当b=c,
k=3,
∴则△ABC的周长=2+3+3=8,
当b=2,c=3或c=2,b=3
则k=2,
则△ABC的周长=2+2+3=7,
故△ABC的周长是7或8.
(x-3)(x-k)=0,
则x1=3,x2=k,
当b=c,
k=3,
∴则△ABC的周长=2+3+3=8,
当b=2,c=3或c=2,b=3
则k=2,
则△ABC的周长=2+2+3=7,
故△ABC的周长是7或8.
点评:本题考查了解一元二次方程-因式分解法:先把方程右边变形为0,然后把方程左边进行因式分解,这样把一元二次方程转化为两个一元一次方程,再解一次方程可得到一元二次方程的解.也考查了解等腰三角形的性质.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
已知等腰△ABC的周长为18cm,BC=8cm,若△ABC≌△A′B′C′,则△A′B′C′中一定有一条边等于( )
| A、7cm | B、2cm或7cm | C、5cm | D、2cm或5cm |
 如图,已知等腰△ABC的一腰AB长为4厘米,过底边BC上任意一点D作两腰的平行线,分别交两腰于E、F,则四边形AEDF的周长为( )
如图,已知等腰△ABC的一腰AB长为4厘米,过底边BC上任意一点D作两腰的平行线,分别交两腰于E、F,则四边形AEDF的周长为( )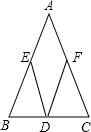 如图,已知等腰△ABC的一腰AB长为4厘米,过底边BC上任意一点D作两腰的平行线,分别交两腰于E、F,则四边形AEDF的周长为
如图,已知等腰△ABC的一腰AB长为4厘米,过底边BC上任意一点D作两腰的平行线,分别交两腰于E、F,则四边形AEDF的周长为