题目内容
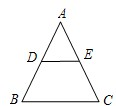
 如图,已知等腰△ABC的一腰AB长为4厘米,过底边BC上任意一点D作两腰的平行线,分别交两腰于E、F,则四边形AEDF的周长为( )
如图,已知等腰△ABC的一腰AB长为4厘米,过底边BC上任意一点D作两腰的平行线,分别交两腰于E、F,则四边形AEDF的周长为( )分析:根据平行线性质得出∠EDB=∠C,∠FDC=∠B,根据∠B=∠C推出∠EDB=∠B,∠FDC=∠C,推出DE=BE,DF=FC,求出四边形AEDF的周长是AE+ED+DF+AF=AB+AC,即可求出答案.
解答:解:∵DE∥AC,DF∥AB,
∴∠EDB=∠C,∠FDC=∠B,
∵AB=AC,
∴∠B=∠C,
∴∠EDB=∠B,∠FDC=∠C,
∴DE=BE,DF=FC,
∴四边形AEDF的周长是AE+ED+DF+AF
=AE+BE+CF+AF
=AB+AC
=2AB
=2×4
=8厘米.
故选B.
∴∠EDB=∠C,∠FDC=∠B,
∵AB=AC,
∴∠B=∠C,
∴∠EDB=∠B,∠FDC=∠C,
∴DE=BE,DF=FC,
∴四边形AEDF的周长是AE+ED+DF+AF
=AE+BE+CF+AF
=AB+AC
=2AB
=2×4
=8厘米.
故选B.
点评:本题考查了平行线的性质,等腰三角形的性质和判定的应用,注意:等角对等边,等边对等角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知等腰△ABC的面积为8cm2,点D,E分别是AB,AC边的中点,则梯形DBCE的面积为
如图,已知等腰△ABC的面积为8cm2,点D,E分别是AB,AC边的中点,则梯形DBCE的面积为 如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连接AB,且有AB=DB.
如图,已知等腰三角形ADC,AD=AC,B是线段DC上的一点,连接AB,且有AB=DB. (2010•西藏)如图,已知等腰△ABC,AC=BC=10,AB=12,以BC为直径作⊙O交AB点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
(2010•西藏)如图,已知等腰△ABC,AC=BC=10,AB=12,以BC为直径作⊙O交AB点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E. 如图,已知等腰△ABC中,AB=AC,P、Q分别为AC、AB上的点,且AP=PQ=QB=BC,则∠PCQ的度数为( )
如图,已知等腰△ABC中,AB=AC,P、Q分别为AC、AB上的点,且AP=PQ=QB=BC,则∠PCQ的度数为( ) 如图,已知等腰Rt△ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于E,
如图,已知等腰Rt△ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于E,