题目内容
【题目】完成下面的证明:
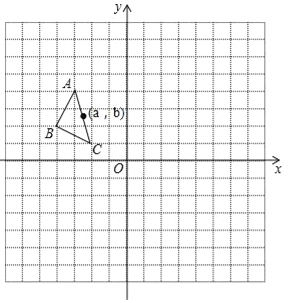
已知:如图,AB∥DE,求证:∠D+∠BCD﹣∠B=180°,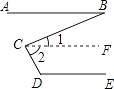
证明:过点C作CF∥AB.
∵AB∥CF(已知),
∴∠B=().
∵AB∥DE,CF∥AB( 已知 ),
∴CF∥DE ()
∴∠2+=180° ()
∵∠2=∠BCD﹣∠1,
∴∠D+∠BCD﹣∠B=180° ().
【答案】∠1;两直线平行,内错角相等;平行于同一条直线的两条直线平行;∠D;两直线平行,同旁内角互补;等量代换
【解析】证明:过点C作CF∥AB,
∵AB∥CF(已知),
∴∠B=∠1(两直线平行,内错角相等),
∵AB∥DE,CF∥AB( 已知 ),
∴CF∥DE (平行于同一条直线的两条直线平行),
∴∠2+∠D=180° (两直线平行,同旁内角互补),
∵∠2=∠BCD﹣∠1,
∴∠D+∠BCD﹣∠B=180° (等量代换),
所以答案是:∠1,两直线平行,内错角相等,平行于同一条直线的两条直线平行,∠D,两直线平行,同旁内角互补,等量代换.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目