题目内容
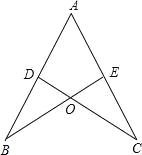
【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证:AD=AE;
(2)若AB=10,AE=6,求BO的长.
【答案】(1)证明参见解析;(2)5.
【解析】
试题分析:(1)欲证明AD=AE,只要证明△ADC≌△AEB即可.(2)先利用勾股定理求出BE,再证明△BDO∽△BEA,得![]() ,由此即可解决问题.
,由此即可解决问题.
试题解析:(1)如图:∵CD⊥AB,BE⊥AC,∴∠ADC=∠AEB=90°,在△ADC和△AEB中,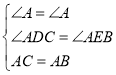 ,∴△ADC≌△AEB(AAS),∴AD=AE.(2)∵AD=AE,AE=6,AB=10,∴BD=10﹣6=4,在Rt△ABE中,BE=
,∴△ADC≌△AEB(AAS),∴AD=AE.(2)∵AD=AE,AE=6,AB=10,∴BD=10﹣6=4,在Rt△ABE中,BE=![]() =
=![]() =8,∵∠B=∠B,∠BDO=∠AEB=90°,∴△BDO∽△BEA,∴
=8,∵∠B=∠B,∠BDO=∠AEB=90°,∴△BDO∽△BEA,∴![]() ,∴
,∴![]() =
=![]() ,∴BO=5.
,∴BO=5.

练习册系列答案
相关题目
