题目内容
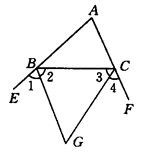
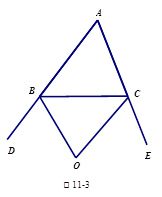
请完成下面的说明:【小题1】如图①所示,△ABC的外角平分线交于G,试说明∠BGC=90°-
 ∠A. 说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____. 根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.根据角平分线的意义,可知∠2+∠3=
∠A. 说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____. 根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.根据角平分线的意义,可知∠2+∠3= (∠EBC+∠FCB)=
(∠EBC+∠FCB)= (180°+∠_____)=90°+
(180°+∠_____)=90°+ ∠_______.所以∠BGC=180°-(∠2+∠3)=90°-∠____
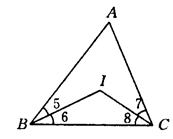
∠_______.所以∠BGC=180°-(∠2+∠3)=90°-∠____【小题2】如图②所示,若△ABC的内角平分线交于点I,试说明∠BIC=90°+
 ∠A.
∠A.【小题3】用(1),(2)的结论,你能说出∠BGC和∠BIC的关系吗?(直接写出结论)


【小题1】A A A A A A
【小题2】说明:根据三角形内角和等于180°,
可得∠ABC+∠ACB=180°-∠A,------------5分
根据角平分线的意义,有
∠6+∠8=
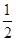 (∠ABC+∠ACB)=
(∠ABC+∠ACB)=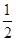 (180°-∠A)=90°-
(180°-∠A)=90°-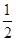 ∠A,--------7分
∠A,--------7分所以∠BIC=180°-(∠6+∠8)
=180°-(90°-
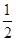 ∠A)=90°+
∠A)=90°+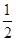 ∠A, --------------------------10分
∠A, --------------------------10分即∠BIC=90°+
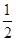 ∠A.
∠A.【小题3】互补.---------2分解析:
利用三角形内角和为180°以及平行线的性质证明

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案
相关题目
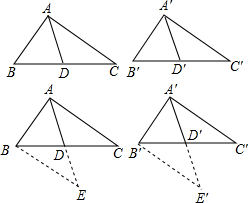 (2013•莒南县一模)【典型练习】如果两个三角形有两条边和其中一边上的中线对应相等,那么这两个三角形全等.(无需证明)
(2013•莒南县一模)【典型练习】如果两个三角形有两条边和其中一边上的中线对应相等,那么这两个三角形全等.(无需证明)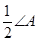 ,理由如下:
,理由如下: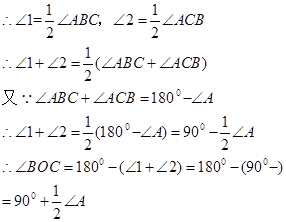



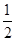 ∠A. 说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____. 根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.根据角平分线的意义,可知∠2+∠3=
∠A. 说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____. 根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.根据角平分线的意义,可知∠2+∠3=