题目内容
【题目】如图,抛物线![]() 与
与![]() 轴交于两点
轴交于两点![]() 和
和![]() 与
与![]() 轴交于点
轴交于点![]() 动点
动点![]() 沿
沿![]() 的边
的边![]() 以每秒
以每秒![]() 个单位长度的速度由起点
个单位长度的速度由起点![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 的另一边
的另一边![]() 于点
于点![]() 将
将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,设点
处,设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.

(1)求抛物线的解析式;
(2)N为抛物线上的点(点![]() 不与点
不与点![]() 重合)且满足
重合)且满足![]() 直接写出
直接写出![]() 点的坐标;
点的坐标;
(3)是否存在某一时刻![]() ,使
,使![]() 的面积最大,若存在,求出
的面积最大,若存在,求出![]() 的值和最大面积;若不存在,请说明理由.
的值和最大面积;若不存在,请说明理由.
【答案】(1)![]() ;(2)(-5,3)或(
;(2)(-5,3)或(![]() ,-3)或(
,-3)或(![]() ,-3);(3)存在,
,-3);(3)存在,![]() 时,
时,![]() 有最大值为
有最大值为![]() .
.
【解析】
(1)把A(-3,0),B(1,0)代入y=ax2+bx+3,得到关于a、b的二元一次方程组,解方程组即可得到结论;
(2)由抛物线解析式求出C(0,3),根据同底等高的两个三角形面积相等,可知N点纵坐标的绝对值等于3,将y=±3分别代入二次函数解析式,求出x的值,进而得到N点的坐标;
(3)由于点D在y轴的右侧时,过点![]() 作
作![]() 轴的垂线,无法与
轴的垂线,无法与 ![]() 的另一边
的另一边![]() 相交,所以点D在y轴左侧,根据题意求出直线AC的解析式及E,D,F的坐标,然后根据三角形面积求得
相交,所以点D在y轴左侧,根据题意求出直线AC的解析式及E,D,F的坐标,然后根据三角形面积求得![]() 与t的函数关系式,然后利用二次函数的性质求最值即可.
与t的函数关系式,然后利用二次函数的性质求最值即可.
解:(1)把A(-3,0),B(1,0)代入y=ax2+bx+3中,得
![]() ,解得
,解得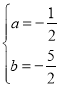 ,
,
∴抛物线的解析式为:![]() ,
,
(2)∵抛物线![]() 与y轴交于点C,
与y轴交于点C,
∴C(0,3).
∵N为抛物线上的点(点![]() 不与点
不与点![]() 重合)且S△NAB=S△ABC,
重合)且S△NAB=S△ABC,
∴设N(x,y),则|y|=3.
把y=3代入![]() ,得
,得![]() ,解得x=0或-5,
,解得x=0或-5,
x=0时N与C点重合,舍去,
∴N(-5,3);
把y=-3代入![]() ,得
,得![]() ,解得
,解得![]()
∴N(![]() ,-3)或(
,-3)或(![]() ,-3).
,-3).
综上所述,所求N点的坐标为(-5,3)或(![]() ,-3)或(
,-3)或(![]() ,-3);
,-3);
(3)存在.
由题意可知,∵过点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 的另一边
的另一边![]() 于点
于点![]()
∴点D必在y轴的左侧.
∵AD=2t,
∴由折叠性质可知DF=AD=2t,
∴OF=3-4t,
∴D(2t-3,0),
∵设直线AC的解析式为:![]() ,将A(-3,0)和C(0,3)代入解析式得
,将A(-3,0)和C(0,3)代入解析式得![]() ,解得
,解得![]()
∴直线AC的解析式为:![]()
∴E(2t-3,2t).
∴![]()
![]()
∵-4<0
![]() 时,
时,![]() 有最大值为
有最大值为![]() .
.


【题目】校学生会对七年级部分学生的课外阅读量进行了随机调查,整理调查结果,并根据调查结果绘制了不完整的图表,如图所示:
本数(本) | 频数(人数) | 频率 |
5 | a | 0.3 |
6 | 10 | 0.2 |
7 | 20 | b |
8 | 5 | 0.1 |
合计 | c | 1 |
(1)统计表中的b= ,c= ;请将频数分布直方图补充完整.
(2)所有被调查学生课外阅读的平均本数为 本,课外阅读书本数的中位数为 本.
(3)若该校七年级共有1200名学生,估计该校七年级学生课外阅读6本及以下的人数为 人.