题目内容
在矩形ABCD中，已知E是BC的中点，∠BAE=30°，AE=2，则AC=
- A.3
- B.2
- C.
- D.
C
分析：应先利用相应的三角函数求得AB，BC长，进而可利用勾股定理求得AC长．
解答：在直角△ABE中，∠BAE=30°．
∴BE=
AE=1，AB=AE•cos∠BEA=．
∴BC=2BE=2．
在直角△ABC中利用勾股定理得到：AC=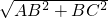
=．
故选C．
点评：本题主要运用了三角函数，直角三角形有一个锐角是30°，30°的锐角所对的直角边等于斜边的一半．
分析：应先利用相应的三角函数求得AB，BC长，进而可利用勾股定理求得AC长．
解答：在直角△ABE中，∠BAE=30°．
∴BE=
AE=1，AB=AE•cos∠BEA=．∴BC=2BE=2．
在直角△ABC中利用勾股定理得到：AC=
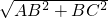=．故选C．
点评：本题主要运用了三角函数，直角三角形有一个锐角是30°，30°的锐角所对的直角边等于斜边的一半．
练习册系列答案
阅读快车系列答案
相关题目
在矩形ABCD中，已知E是BC的中点，∠BAE=30°，AE=2，则AC=（ ）
| A、3 | ||
B、2
| ||
C、
| ||
D、
|
如图，在矩形ABCD中，已知AB=2，BC=3，点E为AD边上一动点（不与A、D重合），连接CE，作EF⊥CE交AB边于F
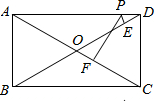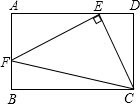
如图，在矩形ABCD中，已知AD=15，AB=8，P是AD边上任意一点，PE⊥BD，PF⊥AC，E，F分别是垂足，那么PE+PF=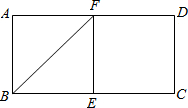
如图，在矩形ABCD中，已知AB=1，BC=2，∠ABC的平分线交AD于点F，E为BC的中点，连接EF．