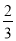Question

如果三角形有一边上的中线恰好等于这边的长，那么称这个三角形为“匀称三角形”．

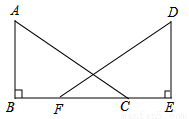
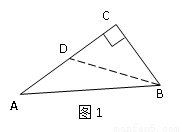
（1）已知：如图1，在△ABC中，∠C=90°，．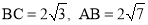

求证：△ABC是“匀称三角形”；

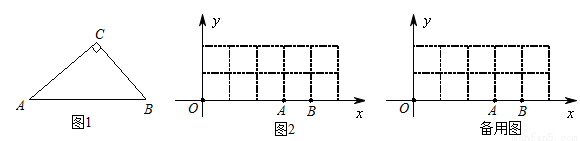
（2）在平面直角坐标系xoy中，如果三角形的一边在x轴上，且这边的中线恰好等于这边的长，我们又称这个三角形为“水平匀称三角形”．如图2，现有10个边长是1的小正方形组成的长方形区域记为G, 每个小正方形的顶点称为格点，A（3，0），B（4，0），若C、D（C、D两点与O不重合）是x轴上的格点，且点C在点A的左侧．在G内使△PAC与△PBD都是“水平匀称三角形”的点P共有几个？其中是否存在横坐标为整数的点P，如果存在请求出这个点P的坐标，如果不存在请说明理由．

 

 

Answer 1

（1）证明见解析；（2）4个，存在，（3，）．

【解析】

试题分析：（1）应用勾股定理求出AC和它的中线长，根据匀称三角形的定义即可证得．

（2）根据匀称三角形的定义求解即可．

试题解析：（1） 如图1，作AC边的中线BD交AC于点D，

∵∠C=90°，BC= 2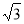，AB = 2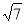，∴AC = 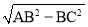= 4．

∴AD=CD=2，BD =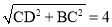 ．∴AC = BD．

∴ △ABC是“匀称三角形”．

（2）①在G内使△PAC与△PBD都是“水平匀称三角形”的点P共有4个 ．

②在G内使△PAC与△PBD都是“水平匀称三角形”的点P中，存在横坐标为整数的点P．

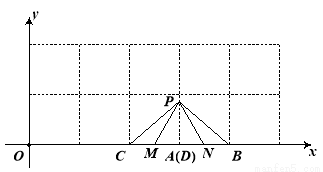
如图，当C点坐标为（2，0），D点坐标为（3，0）与A重合时，△PAC与△PBD是水平匀称三角形．

∵A（3，0），C（2，0），B（4，0），D（3，0），∴AC＝1，BD＝1．

设PM、PN分别为CA、DB上的中线，

∴AM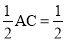＝，AN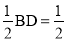＝, ∴AM＝AN=．

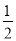∴点A为MN的中点．

∵△PAC与△PBD是“水平匀称三角形”，

∴PM＝AC＝1，PN＝BD＝1．∴PM＝PN=1．

∴PA⊥MN，即PA与x轴垂直．

∵A（3，0），∴P点横坐标为整数3．

在Rt△PMA中，PM＝1，AM=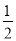，∴PA＝．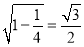

∴P（3，）．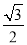

∴当C点坐标为（2，0），D点坐标为（3，0）与A重合时，△PAC与△PBD是水平匀称三角形且P点横坐标为整数．

考点：1．新定义和阅读理解型问题；2．勾股定理；3．点的坐标．