题目内容
某校组织七年级学生到军营训练,为了喝水方便,要求每个学生各带一只水杯,几个学生可以合带一个水壶.可临出发前 ,带队老师发现有51名同学没带水壶和水杯,于是老师拿出260元钱并派两名同学去附近商店购买.该商店有大小不同的甲、乙两种水壶,并且水壶与水杯必须配套购买,每个甲种水壶配4只杯子,每套20元;每个乙种水壶配6只杯子,每套28元.若需购买水壶10个,设购买甲种水壶x个,购买的总费用为y(元)。
(1)求出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)请你帮助设计所有可能的购买方案,并写出最省钱的购买方案及最少费用。
(1)求出y与x之间的函数关系式(不必写出自变量x的取值范围);
(2)请你帮助设计所有可能的购买方案,并写出最省钱的购买方案及最少费用。
解:(1) ,
,
∴y与x的函数关系式为 ;
;
(2)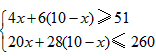
解得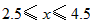 ,
,
∵x为非负整数,
∴x=3或4,
∴有两种购买方案,
第一种:买甲种水壶3个,乙种水壶7个;
第二种:买甲种水壶4个,乙种水壶6个,
∵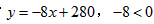 ,
,
∴y随x的增大而减小,
∴当x=4时,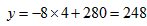 (元),
(元),
答:有两种购买方案.第一种:买甲种水壶3个,乙种水壶7个;第二种:买甲种水壶4个,乙种水壶6个.其中最省钱的方案是第二种,最少费用是248元。
 ,
,∴y与x的函数关系式为
 ;
;(2)
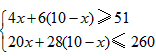
解得
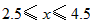 ,
,∵x为非负整数,
∴x=3或4,
∴有两种购买方案,
第一种:买甲种水壶3个,乙种水壶7个;
第二种:买甲种水壶4个,乙种水壶6个,
∵
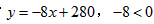 ,
,∴y随x的增大而减小,
∴当x=4时,
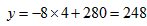 (元),
(元),答:有两种购买方案.第一种:买甲种水壶3个,乙种水壶7个;第二种:买甲种水壶4个,乙种水壶6个.其中最省钱的方案是第二种,最少费用是248元。

练习册系列答案
相关题目