Question

【题目】阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.

已知: 如图,AM,BN,CP 是△ABC 的三条角平分线

求证;AM,BN.CP 交于一点

证明:如图，设AM,BN 交于点0,过点0 分别作OD⊥BC,OF⊥AB,垂足分别为点D,E,F.

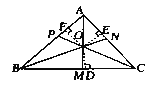
∵O 是∠BAC 角平分线AM上的一点( )

∴OE = OF( )

同理,0D= OF.

∴OD = OE( )

∵CP 是∠ACB 的平分线( )

∴在CP上( )

因此，AM.BN,CP 交于一点.

Answer 1

【答案】见解析.

【解析】试题分析：设AM，BN 交于点O，过点O分别作OD⊥BC，OF⊥AB，垂足分别为点D，E，F，

然后证明OD= OE，从而可知点O在角平分线CP上，从而问题得证.

试题解析： 如图，设AM，BN 交于点O，过点O分别作OD⊥BC，OF⊥AB，垂足分别为点D，E，F，

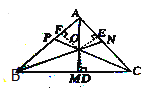
∵O 是∠BAC 角平分线AM 上的一点(已知)，

∴OE=OF( 角平分线上的点到这个角的两边的距离相等)，

同理， OD= OF，

∴OD= OE( 等量代换)，

∵CP是∠ACB的平分线(已知)，

∴O在CP上(角的内部到角的两边距离相等的点在这个角的平分线上)，

因此，AM，BN，CP 交于一点.

故答案为：已知，角平分线上的点到这个角的两边的距离相等，等量代换，已知，角的内部到角的两边距离相等的点在这个角的平分线上.