题目内容
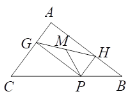
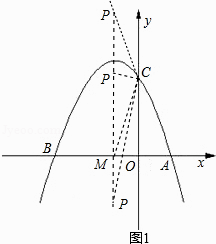
【题目】如图①，已知抛物线y=ax2+bx+3（a≠0）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C．
（1）求抛物线的解析式；
（2）设抛物线的对称轴与x轴交于点M，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由；
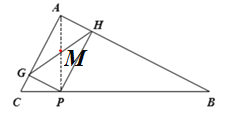
（3）如图②，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．
【答案】
（1）
解：∵抛物线y=ax2+bx+3（a≠0）与x轴交于点A（1，0）和点B（﹣3，0），
∴ 
解得： 
∴所求抛物线解析式为：
y=﹣x2﹣2x+3；
（2）
解：∵抛物线解析式为：
y=﹣x2﹣2x+3，
∴其对称轴为x= 
=﹣1，
∴设P点坐标为（﹣1，a），当x=0时，y=3，
∴C（0，3），M（﹣1，0）
∴当CP=PM时，（﹣1）2+（3﹣a）2=a2，解得a= 
，
∴P点坐标为：P1（﹣1， ）；
∴当CM=PM时，（﹣1）2+32=a2，解得a=± 
，
∴P点坐标为：P2（﹣1， ）或P3（﹣1，﹣ ）；
∴当CM=CP时，由勾股定理得：（﹣1）2+32=（﹣1）2+（3﹣a）2，解得a=6，
∴P点坐标为：P4（﹣1，6）
综上所述存在符合条件的点P，其坐标为P（﹣1， ）或P（﹣1，﹣ ）
或P（﹣1，6）或P（﹣1， ）
（3）
解：过点E作EF⊥x轴于点F，设E（a，﹣a2﹣2a+3）（﹣3＜a＜0）
∴EF=﹣a2﹣2a+3，BF=a+3，OF=﹣a
∴S四边形BOCE= 
BFEF+ （OC+EF）OF
= （a+3）（﹣a2﹣2a+3）+ （﹣a2﹣2a+6）（﹣a）
= 
=﹣ 
+ 
∴当a=﹣ 
时，S四边形BOCE最大，且最大值为 ．
此时，点E坐标为（﹣ ， 
）．
【解析】（1）已知抛物线过A、B两点，可将两点的坐标代入抛物线的解析式中，用待定系数法即可求出二次函数的解析式；（2）可根据（1）的函数解析式得出抛物线的对称轴，也就得出了M点的坐标，由于C是抛物线与y轴的交点，因此C的坐标为（0，3），根据M、C的坐标可求出CM的距离．然后分三种情况进行讨论：①当CP=PM时，P位于CM的垂直平分线上．求P点坐标关键是求P的纵坐标，过P作PQ⊥y轴于Q，如果设PM=CP=x，那么直角三角形CPQ中CP=x，OM的长，可根据M的坐标得出，CQ=3﹣x，因此可根据勾股定理求出x的值，P点的横坐标与M的横坐标相同，纵坐标为x，由此可得出P的坐标．②当CM=MP时，根据CM的长即可求出P的纵坐标，也就得出了P的坐标（要注意分上下两点）．③当CM=CP时，因为C的坐标为（0，3），那么直线y=3必垂直平分PM，因此P的纵坐标是6，由此可得出P的坐标；（3）由于四边形BOCE不是规则的四边形，因此可将四边形BOCE分割成规则的图形进行计算，过E作EF⊥x轴于F，四边形BOCE的面积=三角形BFE的面积+直角梯形FOCE的面积．直角梯形FOCE中，FO为E的横坐标的绝对值，EF为E的纵坐标，已知C的纵坐标，就知道了OC的长．在三角形BFE中，BF=BO﹣OF，因此可用E的横坐标表示出BF的长．如果根据抛物线设出E的坐标，然后代入上面的线段中，即可得出关于四边形BOCE的面积与E的横坐标的函数关系式，根据函数的性质即可求得四边形BOCE的最大值及对应的E的横坐标的值．即可求出此时E的坐标．
