题目内容
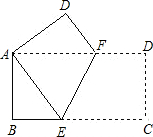 如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是
如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是
- A.

- B.

- C.

- D.
D
分析:根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等和勾股定理求解.
解答:根据折叠的性质知,四边形AFEB与四边形FDCE全等,有EC=AF=AE,
由勾股定理得,AB2+BE2=AE2即42+(8-AE)2=AE2,
解得,AE=AF=5,BE=3,
作EG⊥AF于点G,

则四边形AGEB是矩形,有AG=3,GF=2,GE=AB=4,由勾股定理得EF=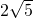 .
.
故选D.
点评:本题利用了:1、折叠的性质;2、矩形的性质.
分析:根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等和勾股定理求解.
解答:根据折叠的性质知,四边形AFEB与四边形FDCE全等,有EC=AF=AE,
由勾股定理得,AB2+BE2=AE2即42+(8-AE)2=AE2,
解得,AE=AF=5,BE=3,
作EG⊥AF于点G,

则四边形AGEB是矩形,有AG=3,GF=2,GE=AB=4,由勾股定理得EF=
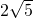 .
.故选D.
点评:本题利用了:1、折叠的性质;2、矩形的性质.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
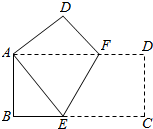 如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是( )
如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是( )A、
| ||
B、2
| ||
C、
| ||
D、2
|
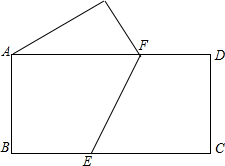
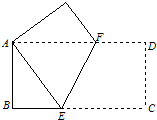 16、如图,将一个边长分别为4、8的长方形纸片ABCD折叠,使C点与A点重合,求EB的长.
16、如图,将一个边长分别为4、8的长方形纸片ABCD折叠,使C点与A点重合,求EB的长.
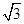 B.
B.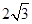 C.
C.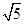 D.
D.
