题目内容
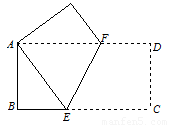
 16、如图,将一个边长分别为4、8的长方形纸片ABCD折叠,使C点与A点重合,求EB的长.
16、如图,将一个边长分别为4、8的长方形纸片ABCD折叠,使C点与A点重合,求EB的长.分析:设BE=x,则AE=EC=8-x,在RT△ABE中运用勾股定理可解出x的值,继而可得出EB的长度.
解答:解:设BE=x,则AE=EC=8-x,
在RT△ABE中,AB2+BE2=AE2,即42+x2=(8-x)2,
解得:x=3,
即EB的长为3.
在RT△ABE中,AB2+BE2=AE2,即42+x2=(8-x)2,
解得:x=3,
即EB的长为3.
点评:本题考查了翻折变换的知识,解答本题需要在RT△ABE中利用勾股定理,关键是根据翻折的性质得到AE=EC这个条件.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
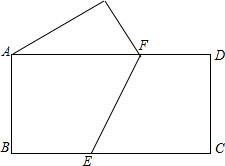
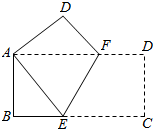 如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是( )
如图,将一个边长分别为4,8的长方形纸片ABCD折叠,使C点与A点重合,则折痕EF的长是( )A、
| ||
B、2
| ||
C、
| ||
D、2
|
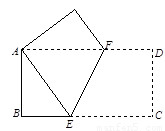
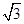 B.
B.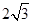 C.
C.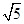 D.
D.